若
，
，则
中元素个数为
| A．0 | B．1 | C．2 | D．3 |
复数
的共轭复数是
A． |
B． |
C．1 | D． |
等差数列
前
项和
，
，则公差d的值为
| A． 2 | B． 3 | C． 4 | D．-3 |
下列函数中，周期为
，且在区间
上单调递增的函数是
A． |
B． |
C． |
D． |
命题
:函数
（
且
）的图像恒过点
；命题
：函数
有两个零点. 则下列说法正确的是
| A．“或”是真命题 |
B．“且”是真命题 |
C． 为假命题 |
D． 为真命题 |
已知
，且
，则锐角
的值（ ）
A． |
B． |
C． |
D． |
正方体ABCD—A1B1C1D1 中，EF是异面直线AC和A1D 的公垂线，则EF和BD1的关系是 （ ）
| A．相交但不垂直 | B．垂直相交 | C．异面 | D．平行 |
若函数
的图象的顶点在第四象限，则其导函数
的图象可能是（ ）
A． B． C． D．
如图，在△ABC中，∠CAB=∠CBA=30°，AC、BC边上的高分别为BD、AE，
则以A、B为焦点，且过D、E的椭圆与双曲线的离心率的倒数和为 （ ） 
A．
B．1 C．2 D．2
设函数
则
的值为 （ ）
| A．a, b中较大的数 | B．a, b中较小的数 | C． a | D．b |
若实数
,
满足约束条件
, 则目标函数
的最小值为______.
已知圆
的参数方程为
为参数)，以原点为极点，
轴的非负半轴为极轴建立极坐标系，直线的极坐标方程为
, 则直线被圆所截得的弦长是 .
在△ABC中，已知
,则
的值是 .
已知椭圆
和双曲线
有公共的焦点，那么双曲线的渐近线方程是 .
将含有3n个正整数的集合M分成元素个数相等且两两没有公共元素的三个集合
A、B、C，其中
，
，
，若A、B、C中的元素满足条件：
，
，
1,2，…，
，则称
为“完并集合”.
（1）若
为“完并集合”，则
的一个可能值为 .（写出一个即可）
（2）对于“完并集合”
，在所有符合条件的集合
中，其元素乘积最小的集合是 .
设F1、F2分别为椭圆C：
=1（a＞b＞0）的左、右两个焦 点。（1）若椭圆C上的点A（1，
）到F1、F2两点的 距离之和等于4，写出椭圆C的方程和焦点坐标；
（2）设点K是（1）中所得椭圆上的动点，求线段F1K的中点的轨迹方程.
如图，三棱锥
中，
底面ABC于B，
=900，
，点E、F分别是PC、AP的中点。
（1）求证：侧面
；
（2）求异面直线AE与BF所成的角；
2005年10月12日，我国成功发射了“神州”六号载人飞船，这标志着中国人民又迈出了具有历史意义的一步。已知火箭的起飞重量M是箭体（包括搭载的飞行器）的重量m和燃料重量x之和。在不考虑空气阻力的条件下，假设火箭的最大速度y关于x的函数关系式为：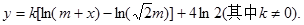
当燃料重量为
吨（e为
自然对数的底数，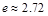
）时，该火箭的最大速度为4（km/s）.
（1）求火箭的最大速度
与燃料重量x吨之间的函数关系式
；
（2）已知该火箭的起飞重量是544吨 ，是应装载多少吨燃料，才能使该火箭的最大飞行速度达到8km/s，顺利地把飞船发送到预定的轨道？
某校高一某班的一次数学测试成绩（满分100分）的茎叶图和频率分布直方图都受到不同程度的污染，但可见部分如下，据此解答如下问题：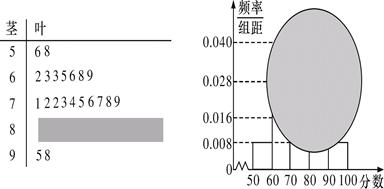
(Ⅰ) 求分数在[50,60)的频率及全班人数；
(Ⅱ) 求分数在[80,90)之间的频数，并计算频率分布直方图中[80,90)间的矩形的高；
（Ⅲ）若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况，在抽取的试卷中，求至少有一份分数在[90,100]之间的概率.
设椭圆C：
过点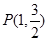
, 且离心率
．
(Ⅰ)求椭圆Ｃ的方程；
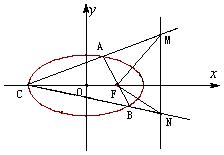
(Ⅱ)过右焦点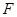
的动直线交椭圆于点
，设椭圆的左顶点为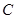
连接
且交直线
于
，若以MN为直径的圆恒过右焦点F，求
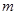的值