若集合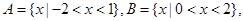 则集合
则集合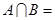 ( )
( )
A.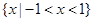 |
B.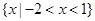 |
C.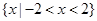 |
D.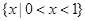 |
已知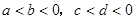 ,那么下列判断中正确的是( )
,那么下列判断中正确的是( )
A.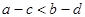 |
B.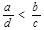 |
C.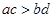 |
D.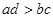 |
满足条件a=4,b=3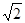 ,A=45°的
,A=45°的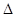 ABC的个数是( )
ABC的个数是( )
| A.一个 | B.两个 | C.无数个 | D.零个 |
如果圆x2+y2+Dx+Ey+F=0与x轴切于原点, 那么( )
| A.D=0,E≠0, F≠0; | B.E=F=0,D≠0; |
| C.D="F=0," E≠0; | D.D=E=0,F≠0; |
设、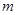 是两条不同的直线,
是两条不同的直线,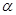 是一个平面,则下列命题正确的是( )
是一个平面,则下列命题正确的是( )
A.若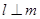 , ,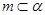 ,则 ,则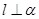 |
B.若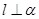 , ,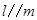 ,则 ,则 |
C.若 , ,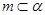 ,则 ,则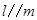 |
D.若 , ,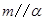 ,则 ,则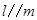 |
如图1, 为正三角形,
为正三角形,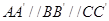 ,
, ,且
,且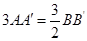

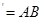 ,则多面体
,则多面体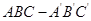 的正视图(也称主视图)是( )
的正视图(也称主视图)是( )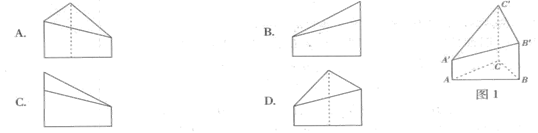
已知点(x,y)在直线x+2y=3上移动,则2x+4y的最小值是( )
| A.8 | B.6 | C.3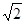 |
D.4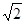 |
已知x1、x2是方程4x2-4mx+m+2=0的两个实根,当x12+x22取最小值时,实数m的值是( )
| A.2 | B.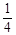 |
C.-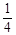 |
D.-1 |
函数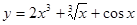 ,则导数
,则导数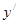 =( )
=( )
A.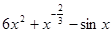 |
B.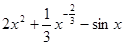 |
C.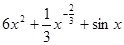 |
D.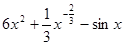 |
已知对任意实数 ,有
,有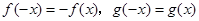 ,且
,且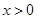 时,
时,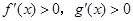 ,则
,则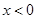 时( )
时( )
A.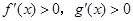 |
B.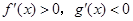 |
C. |
D.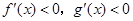 |
在棱长为1的正方体ABCD—A1B1C1D1中,M和N分别为A1B1和BB1的中点,那么直线AM与CN所成角的余弦值是 ( )
A.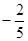 |
B.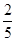 |
C.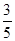 |
D.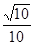 |
设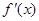 是函数
是函数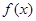 的导函数,将
的导函数,将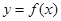 和
和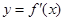 的图象画在同一个直角坐标系中,不可能正确的是( )
的图象画在同一个直角坐标系中,不可能正确的是( )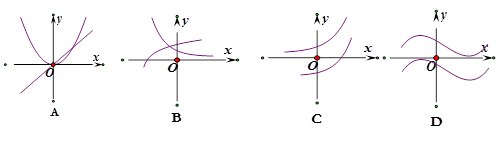
函数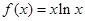 的单调递增区间是________________.
的单调递增区间是________________.
已知函数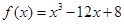 在区间
在区间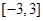 上的最大值与最小值分别为
上的最大值与最小值分别为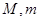 ,则
,则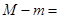 ___________.
___________.
正四棱锥P-ABCD的所有棱长都相等,则侧棱与底面所成的角为 .
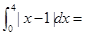 ___________ .
___________ .
已知:以点C (t, 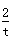 )(t∈R , t ≠ 0)为圆心的圆与
)(t∈R , t ≠ 0)为圆心的圆与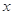 轴交于点O, A,与y轴交于点O, B,其中O为原点.
轴交于点O, A,与y轴交于点O, B,其中O为原点.
(Ⅰ)求证:△OAB的面积为定值;
(Ⅱ)设直线y = –2x+4与圆C交于点M, N,若|OM| = |ON|,求圆C的方程.
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=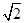 ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点.
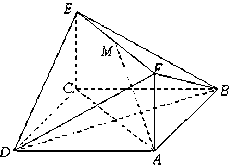
(Ⅰ)求证AM//平面BDE;
(Ⅱ)求二面角A-DF-B的大小;
(Ⅲ)试在线段AC上确定一点P,使得PF与BC所成的角是60°.
设双曲线的顶点为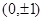 ,该双曲线又与直线
,该双曲线又与直线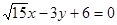 交于
交于 两点,且
两点,且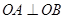 (
(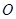 为坐标原点)。
为坐标原点)。
(1)求此双曲线的方程;
(2)求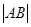
已知函数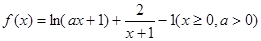 。
。
(1)若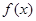 在
在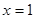 处取得极值,求
处取得极值,求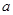 的值;
的值;
(2)求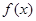 的单调区间;
的单调区间;
(3)若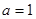 且
且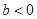 ,函数
,函数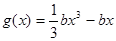 ,若对于
,若对于 ,总存在
,总存在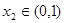 使得
使得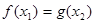 ,求实数
,求实数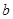 的取值范围。
的取值范围。
如图,线段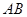 的两个端点
的两个端点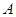 、
、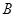 分别分别在
分别分别在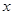 轴、
轴、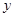 轴上滑动,
轴上滑动,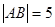 ,点
,点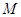 是
是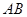 上一点,且
上一点,且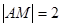 ,点
,点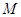 随线段
随线段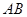 的运动而变化.
的运动而变化.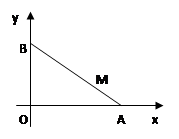
(1)求点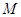 的轨迹方程;
的轨迹方程;
(2)设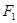 为点
为点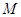 的轨迹的左焦点,
的轨迹的左焦点,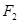 为右焦点,过
为右焦点,过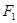 的直线交
的直线交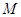 的轨迹于
的轨迹于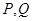 两点,求
两点,求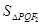 的最大值,并求此时直线
的最大值,并求此时直线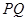 的方程.
的方程.