函数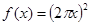 的导数是( )
的导数是( )
A.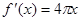 |
B.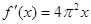 |
C.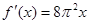 |
D.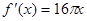 |
积分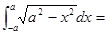 ( )
( )
A.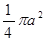 |
B.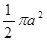 |
C.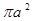 |
D.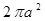 |
曲线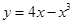 在点(-1,-3)处的切线方程是( )
在点(-1,-3)处的切线方程是( )
A.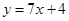 |
B. |
C.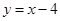 |
D.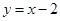 |
设函数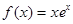 ,则( )
,则( )
A.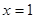 为 为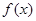 的极大值点 的极大值点 |
B.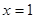 为 为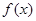 的极小值点 的极小值点 |
C.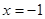 为 为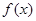 的极大值点 的极大值点 |
D.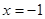 为 为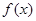 的极小值点 的极小值点 |
如果圆x2+y2+Dx+Ey+F=0与x轴切于原点, 那么( )
| A.D=0,E≠0, F≠0 | B.E=F=0,D≠0 | C.D="F=0," E≠0 | D.D=E=0,F≠0 |
设、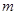 是两条不同的直线,
是两条不同的直线,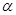 是一个平面,则下列命题正确的是( )
是一个平面,则下列命题正确的是( )
A.若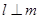 , ,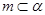 ,则 ,则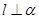 |
B.若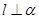 , ,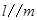 ,则 ,则 |
C.若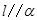 , ,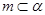 ,则 ,则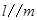 |
D.若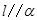 , ,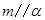 ,则 ,则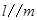 |
已知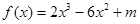 (
(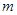 为常数)在
为常数)在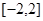 上有最大值
上有最大值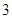 ,那么此函数在
,那么此函数在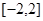 上的最小值为( )
上的最小值为( )
| A.-37 | B.-29 | C.-5 | D.-11 |
当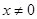 时,有不等式 ( )
时,有不等式 ( )
A.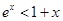 |
B.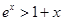 |
C.当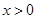 时 时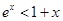 ,当 ,当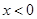 时 时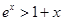 |
D.当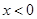 时 时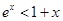 ,当 ,当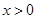 时 时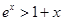 |
曲线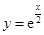 在点
在点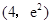 处的切线与坐标轴所围三角形的面积为( )
处的切线与坐标轴所围三角形的面积为( )
A.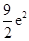 |
B.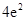 |
C. |
D.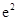 |
关于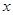 的不等式
的不等式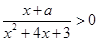 的解为
的解为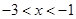 或
或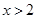 ,则
,则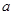 的取值为( )
的取值为( )
| A.2 | B.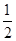 |
C.-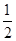 |
D.-2 |
如果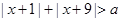 对任意实数x总成立,则a的取值范围是 ( )
对任意实数x总成立,则a的取值范围是 ( )
A.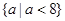 |
B.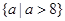 |
C.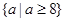 |
D.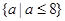 |
已知函数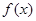 ,
,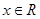 ,且
,且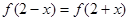 ,当
,当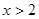 时,
时,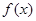 是增函数,设
是增函数,设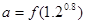 ,
,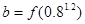 ,
,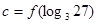 ,则
,则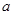 、
、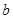 、
、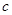 的大小顺序是( )。
的大小顺序是( )。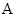 .
. 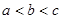
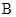 .
. 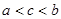
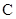 .
. 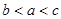
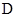 .
. 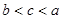
设曲线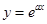 在点
在点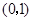 处的切线与直线
处的切线与直线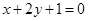 垂直,则
垂直,则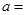 .
.
若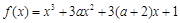 有极大值和极小值,则
有极大值和极小值,则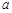 的取值范围是__ .
的取值范围是__ .
函数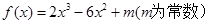 在
在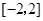 上有最大值3,那么此函数在
上有最大值3,那么此函数在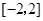 上的最小值为_____
上的最小值为_____
若函数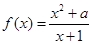 在
在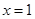 处取极值,则
处取极值,则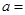 .
.
已知:以点C (t, 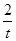 )(t∈R , t ≠ 0)为圆心的圆与
)(t∈R , t ≠ 0)为圆心的圆与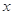 轴交于点O, A,与y轴交于点O, B,其中O为原点.
轴交于点O, A,与y轴交于点O, B,其中O为原点.
(1)求证:△OAB的面积为定值;
(2)设直线y = –2x+4与圆C交于点M, N,若|OM| = |ON|,求圆C的方程.
已知函数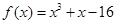 .
.
(1)求曲线 在点
在点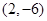 处的切线方程;
处的切线方程;
(2)直线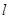 为曲线
为曲线 的切线,且经过原点,求直线
的切线,且经过原点,求直线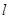 的方程及切点坐标.
的方程及切点坐标.
已知圆C: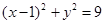 内有一点P(2,2),过点P作直线
内有一点P(2,2),过点P作直线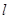 交圆C于A、B两点。
交圆C于A、B两点。
(1)当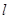 经过圆心C时,求直线
经过圆心C时,求直线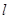 的方程;
的方程;
(2)当弦AB的长为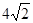 时,写出直线
时,写出直线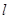 的方程。
的方程。
已知曲线 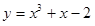 在点
在点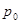 处的切线
处的切线 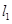 平行直线
平行直线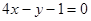 ,且点
,且点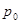 在第三象限.
在第三象限.
(1)求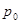 的坐标;
的坐标;
(2)若直线  , 且
, 且 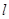 也过切点
也过切点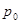 ,求直线
,求直线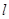 的方程.
的方程.
已知函数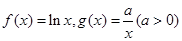 ,设
,设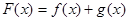
(1)求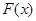 的单调区间;
的单调区间;
(2)若以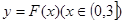 图象上任意一点
图象上任意一点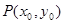 为切点的切线的斜率
为切点的切线的斜率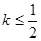 恒成立,求实数
恒成立,求实数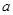 的最小值;
的最小值;
(3)是否存在实数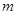 ,使得函数
,使得函数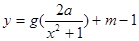 的图象与
的图象与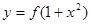 的图象恰好有四个不同的交点?若存在,求出
的图象恰好有四个不同的交点?若存在,求出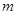 的取值范围,若不存在,说明理由。
的取值范围,若不存在,说明理由。
若存在实常数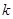 和
和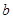 ,使得函数
,使得函数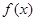 和
和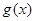 对其定义域上的任意实数
对其定义域上的任意实数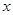 分别满足:
分别满足: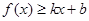 和
和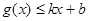 ,则称直线
,则称直线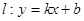 为
为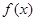 和
和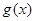 的“隔离直线”.已知
的“隔离直线”.已知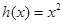 ,
,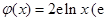 为自然对数的底数).
为自然对数的底数).
(1)求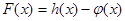 的极值;
的极值;
(2)函数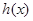 和
和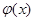 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.