不等式 的解集是 .
的解集是 .
函数 的最小值为 .
的最小值为 .
下图是用同样规格的黑、白两色正方形瓷砖铺设的若干图案,则按此规律第 个图案中需用黑色瓷砖 块.
个图案中需用黑色瓷砖 块.

在 中,
中, ,
, ,
, ,则
,则 = .
= .
已知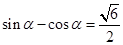 ,则
,则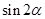 的值等于 .
的值等于 .
在△ 中,已知
中,已知 ,则
,则 = .
= .
若 是等比数列,
是等比数列, ,且公比
,且公比 为整数,则
为整数,则 = .
= .
在 中,若
中,若 ,则
,则 的形状是 .
的形状是 .
已知关于 的不等式
的不等式 的解集为(2,
的解集为(2, ),则
),则 的解集为 .
的解集为 .
在 中,
中, ,
,  ,则
,则 = .
= .
已知实数 为等比数列,
为等比数列, 存在等比中项
存在等比中项 ,
, 的等差中项为
的等差中项为 ,则
,则 .
.
已知 ,则
,则 的值等于 .
的值等于 .
数列 的通项
的通项 ,第2项是最小项,则
,第2项是最小项,则 的取值范围是 .
的取值范围是 .
设 ,且
,且 ,记
,记 中的最大数为
中的最大数为 ,则
,则 的最小值为 .
的最小值为 .
设 是等比数列
是等比数列 的前
的前 项和,且
项和,且 ,
, .
.
(1)求 的通项公式
的通项公式 ;
;
(2)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
已知在 中,角
中,角 所对的边分别为
所对的边分别为 ,且
,且 .
.
(1)求角 ;
;
(2)若 的外接圆半径为2,求
的外接圆半径为2,求 的面积.
的面积.
(1)如图,已知 是坐标平面内的任意两个角,且
是坐标平面内的任意两个角,且 ,证明两角差的余弦公式:
,证明两角差的余弦公式: ;
;
(2)已知 ,且
,且 ,
, ,求
,求 的值.
的值.
如图,某城市设立以城中心 为圆心、
为圆心、 公里为半径的圆形保护区,从保护区边缘起,在城中心
公里为半径的圆形保护区,从保护区边缘起,在城中心 正东方向上有一条高速公路
正东方向上有一条高速公路 、西南方向上有一条一级公路
、西南方向上有一条一级公路 ,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆
,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆 相切的直道
相切的直道 .已知通往一级公路的道路
.已知通往一级公路的道路 每公里造价为
每公里造价为 万元,通往高速公路的道路
万元,通往高速公路的道路 每公里造价是
每公里造价是 万元,其中
万元,其中 为常数,设
为常数,设 ,总造价为
,总造价为 万元.
万元.
(1)把 表示成
表示成 的函数
的函数 ,并求出定义域;
,并求出定义域;
(2)当 时,如何确定A点的位置才能使得总造价最低?
时,如何确定A点的位置才能使得总造价最低?
已知函数
(1)若不等式 的解集为
的解集为 ,求
,求 的取值范围;
的取值范围;
(2)解关于 的不等式
的不等式 ;
;
(3)若不等式 对一切
对一切 恒成立,求
恒成立,求 的取值范围.
的取值范围.
设数列 的前
的前 项和为
项和为 ,且方程
,且方程 有一个根为
有一个根为 ,
, .
.
(1)证明:数列 是等差数列;
是等差数列;
(2)设方程 的另一个根为
的另一个根为 ,数列
,数列 的前
的前 项和为
项和为 ,求
,求 的值;
的值;
(3)是否存在不同的正整数 ,使得
,使得 ,
, ,
, 成等比数列,若存在,求出满足条件的
成等比数列,若存在,求出满足条件的 ,若不存在,请说明理由.
,若不存在,请说明理由.