已知三角形的两边分别为4和10,则此三角形的第三边可能是( )
| A.4 | B.6 | C.8 | D.16 |
如图,下列说法中,正确的是( )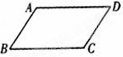
| A.因为∠A+∠D=180°, 所以AB∥CD |
| B.因为∠C+∠D=180°, 所以AB∥CD |
| C.因为∠A+∠D=180°, 所以AD∥BC |
| D.因为∠A+∠C=180°, 所以AB∥CD |
下列计算正确的是( )
A.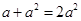 |
B.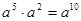 |
C.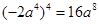 |
D.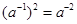 |
下列各式能用平方差公式计算的是( )
A.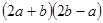 |
B.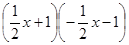 |
C.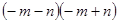 |
D.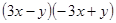 |
若一个三角形三个内角度数的比为11︰7︰3,那么这个三角形是( )
| A.直角三角形 | B.锐角三角形 | C.等边三角形 | D.钝角三角形 |
已知代数式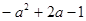 ,无论
,无论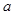 取任何值,它的值一定是( )
取任何值,它的值一定是( )
| A.正数 | B.零或负数 | C.零或正数 | D.负数 |
如图是一块长方形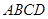 的场地,长
的场地,长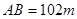 ,宽
,宽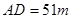 ,从
,从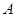 、
、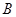 两处入口的中路宽都为
两处入口的中路宽都为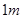 ,两小路汇合处路宽为
,两小路汇合处路宽为 ,其余部分种植草坪,则草坪面积为( )
,其余部分种植草坪,则草坪面积为( )
A.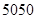 m2 m2 |
B.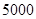 m2 m2 |
C. m2 m2 |
D. m2 m2 |
如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE的外部时,则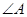 与
与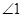 和
和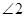 之间有一种数量关系始终保持不变,你发现的规律是( )
之间有一种数量关系始终保持不变,你发现的规律是( )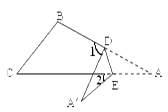
A. |
B.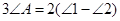 |
C.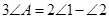 |
D.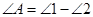 |
已知一个多边形的每一个外角都是300,则这个多边形的边数为 .
甲型H7N9流感病毒的直径大约为0.0000000081米,用科学记数法表示为 .
若 ,则
,则 = .
= .
把多项式 提出一个公因式
提出一个公因式 后,另一个因式是 .
后,另一个因式是 .
已知 ,
, ,则
,则 .
.
 =___ ___.
=___ ___.
若凸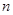 边形的内角和为1260°,则
边形的内角和为1260°,则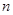 = .
= .
若 ,
,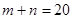 ,则
,则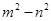 的值为 .
的值为 .
如图所示,是用一张长方形纸条折成的.如果∠1=126°,那么∠2= 。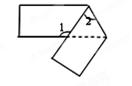
如图,在△ABC中,已知点D、E、F分别是BC、AD、BE上的中点,且△ABC的面积为8㎝2,则△BCF的面积为 ㎝2.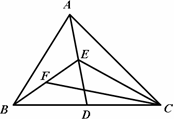
(1)|―3|―( ―
― )
) +
+ +(-1)3
+(-1)3
(2)a·a2·a3+(-2a3)2-a8÷a2
(3)(3-4y)(3+4y)
(4)(x-2)(x+3)-(x+3)2
因式分解
(1) (2)
(2)
(3)  (4)
(4)

如图,在△ABC中,∠BAC是钝角,请画出AB边上的高CD,BC边上的中线AE,∠BCA的平分线CF.(请保留作图痕迹)
如图,每个正方形的边长都为1,请画出小船向左平移6格的图形,并计算平移后小船的面积.小船的面积为____ ___(不写过程)
已知 ,求
,求 的值。
的值。
如图,AB∥CD,∠B = 72°,∠D = 32°,求∠F的度数。
如图,已知∠ABC+∠ECB=1800,∠P=∠Q,
(1)AB与ED平行吗?为什么?
(2)∠1与∠2是否相等?说说你的理由。
图是一个长为 、宽为
、宽为 的长方形, 沿图中虚线用剪刀均分成四块小长方形, 然后按图2的形状拼成一个正方形.
的长方形, 沿图中虚线用剪刀均分成四块小长方形, 然后按图2的形状拼成一个正方形.

(1)你认为图2的阴影部分的正方形的边长等于 ;
(2)请用两种不同的方法求图2阴影部分的面积;
(3)观察图,你能写出下列三个代数式之间的等量关系吗?
代数式:
如图,在△ABC中,∠A=60°,点E是两条内角平分线的交点,点F是两条外角平分线,点A1是内角∠ABC、外角∠ACD平分线的交点的交点.
(1)求∠A1EC的度数;
(2)求∠BFC的度数;
(3)探索∠A1与∠A的数量关系,并说明理由;
(4)若∠A=100°,在(3)的情况下,作∠A1BC与∠A1CD的平分线交于点A2,以此类推,∠AnBC与∠AnCD的平分线交于点An,求∠An的度数。(直接写出结果)