若函数 且
且 ,则
,则
已知直线 和圆
和圆 ,点
,点 在直线
在直线 上,
上, ,
, 为圆
为圆 上两点,在
上两点,在 中,
中, ,
, 过圆心
过圆心 ,则点
,则点 横坐标范围为 .
横坐标范围为 .
在坐标平面上有两个区域 和
和 ,
, 为
为 ,
, 是随
是随 变化的区域,它由不等式
变化的区域,它由不等式 所确定,
所确定, 的取值范围是
的取值范围是 ,则
,则 和
和 的公共面积是函数
的公共面积是函数 .
.
使不等式 对一切正整数
对一切正整数 都成立的最小正整数
都成立的最小正整数 的值为 .
的值为 .
椭圆
 上任意两点
上任意两点 ,
, ,若
,若 ,则乘积
,则乘积 的最小值为 .
的最小值为 .
若方程 仅有一个实根,那么
仅有一个实根,那么 的取值范围是 .
的取值范围是 .
一个由若干行数字组成的数表,从第二行起每一行中的数字均等于其肩上的两个数之和,最后一行仅有一个数,第一行是前 个正整数按从小到大排成的行,则最后一行的数是 (可以用指数表示)
个正整数按从小到大排成的行,则最后一行的数是 (可以用指数表示)
某车站每天 ,
, 都恰有一辆客车到站,但到站的时刻是随机的,且两者到站的时间是相互独立的,其规律为
都恰有一辆客车到站,但到站的时刻是随机的,且两者到站的时间是相互独立的,其规律为
| 到站时刻 |
  |
  |
  |
| 概率 |
 |
 |
 |
一旅客 到车站,则它候车时间的数学期望为 (精确到分).
到车站,则它候车时间的数学期望为 (精确到分).
(本小题满分14分)设直线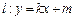 (其中
(其中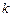 ,
, 为整数)与椭圆
为整数)与椭圆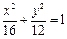 交于不同两点
交于不同两点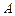 ,
,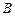 ,与双曲线
,与双曲线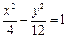 交于不同两点
交于不同两点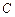 ,
,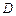 ,问是否存在直线
,问是否存在直线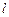 ,使得向量
,使得向量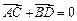 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由.
(本小题15分)已知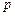 ,
,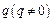 是实数,方程
是实数,方程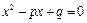 有两个实根
有两个实根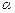 ,
,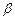 ,数列
,数列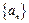 满足
满足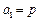 ,
,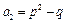 ,
,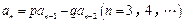
(Ⅰ)求数列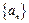 的通项公式(用
的通项公式(用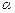 ,
,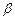 表示);
表示);
(Ⅱ)若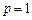 ,
,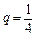 ,求
,求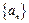 的前
的前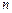 项和.
项和.
(本小题满分15分)求函数 的最大和最小值.
的最大和最小值.