若命题p的逆命题是q,命题p的逆否命题是r, 则命题q与r的关系是( )
| A.互为逆命题 | B.互为否命题 | C.互为逆否命题 | D.不能确定 |
“x>1”是“ >x”的( )
>x”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
若命题p 假,且命题
假,且命题 为假,则( )
为假,则( )
A.p 为假 为假 |
B.q为真 | C.q为假 | D.不能判断q的真假 |
若椭圆的短轴长为4 ,它的一个焦点是(2
,它的一个焦点是(2 ,0),则该椭圆的标准方程是( )
,0),则该椭圆的标准方程是( )
A. =1 =1 |
B.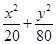 ="1" ="1" |
C.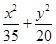 ="1" ="1" |
D. =1 =1 |
椭圆 =1上一点M到左焦点F
=1上一点M到左焦点F 的距离为2, N是MF
的距离为2, N是MF 的中点,则
的中点,则 =( )
=( )
| A.2 | B.4 | C.6 | D. |
双曲线方程为x -2y
-2y =1.则它的右焦点坐标是( )
=1.则它的右焦点坐标是( )
A.( ,0) ,0) |
B.( ,0) ,0) |
C.( ,0) ,0) |
D.( ,0) ,0) |
若抛物线顶点为坐标原点,对称轴为x轴,焦点在3x-4y-12=0上,那么抛物线方程是( )
A.y =16x =16x |
B.y =-16x =-16x |
C.y =12x =12x |
D.y =-12x =-12x |
设 是函数
是函数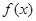 的导函数,将
的导函数,将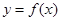 和
和 的图象画在同一个直角坐标系中,不可能正确的是( )
的图象画在同一个直角坐标系中,不可能正确的是( )
曲线 +
+ =1.(m<6) 与
=1.(m<6) 与 +
+ =1.(5<m<9)的( )
=1.(5<m<9)的( )
| A.准线相同 | B.离心率相同 | C.焦点相同 | D.焦距相同 |
曲线f(x)=x㏑x在点x=1处的切线方程是( )
| A.y=2x+2 | B.y=2x-2 | C.y=x-1 | D.y=x+1 |
特称命题:“ x
x R, x
R, x -2x+1=0”的否定是_________.
-2x+1=0”的否定是_________.
双曲线3x -y
-y =9的渐近线方程是 .
=9的渐近线方程是 .
若抛物线y =2px的焦点与椭圆
=2px的焦点与椭圆 +
+ =1的右焦点重合,则p的值为 .
=1的右焦点重合,则p的值为 .
函数y= x-cosx,x
x-cosx,x [-
[- ,
, ]的最大值是_________.
]的最大值是_________.
若方程 +
+ =1所表示的曲线为C,则下面四个命题
=1所表示的曲线为C,则下面四个命题
①若C为椭圆,则1<t<4 ;②若C为双曲线,则t>4或t<1;
③曲线C不可能是圆;④若C为椭圆, 且长轴在x轴上,则1<t<
且长轴在x轴上,则1<t<
其中真命题的序号是_________.
写出命题“正数a的平方大于零”的逆命题,否命题,逆否命题,并判断这三种命题的真假。
已知f(x)=(x+1)(x-1)(x+2),求f′(x),f′(2),[f(2)]′
设双曲线与椭圆 +
+ =1有公共的焦点,且与椭圆相交,它们的交点中一个交点的纵坐标是4,求双曲线的标准方程。
=1有公共的焦点,且与椭圆相交,它们的交点中一个交点的纵坐标是4,求双曲线的标准方程。
过椭圆 +
+ =1内一点M(2,1)引一条弦,使弦被M点平分,求此弦所在直线方程。
=1内一点M(2,1)引一条弦,使弦被M点平分,求此弦所在直线方程。
已知函数f(x)=-x +3x
+3x +9x+a
+9x+a
⑴求f(x)的单调递减区间;⑵若f(x)在区间[-2,2]上的最大值为20,求它在该区间上的最小值。
如图所示,O为坐标原点,过点P(2,0)且斜率为k的直线L交抛物线y =2x于M(x
=2x于M(x ,y
,y ),N(x
),N(x ,y
,y )两点. ⑴写出直线L的方程;⑵求x
)两点. ⑴写出直线L的方程;⑵求x x
x 与y
与y y
y 的值;⑶求证:OM⊥ON
的值;⑶求证:OM⊥ON