若集合 ,则
,则 ( ).
( ).
A. |
B. |
C. |
D. |
已知数列{ an }满足a1= ,且对任意的正整数m,n,都有am+n= am + an,则
,且对任意的正整数m,n,都有am+n= am + an,则 等于( )
等于( )
A. |
B. |
C. |
D.2 |
若 是纯虚数,则
是纯虚数,则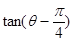 的值为( ).
的值为( ).
A. |
B. |
C.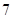 |
D. 或 或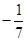 |
若两个非零向量 ,
, 满足
满足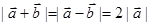 ,则向量
,则向量 与
与 的夹角为( )
的夹角为( )
A. |
B.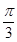 |
C. |
D. |
已知某三棱锥的三视图(单位:Cm)如图所示,则该三棱锥的体积是( )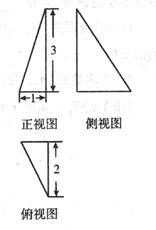
| A. 6cm3 | B.2cm3 | C.3 cm3 | D.1cm3 |
若在区域 内任取一点P,则点P恰好在单位圆
内任取一点P,则点P恰好在单位圆 内的概率为( )
内的概率为( )
A. |
B.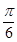 |
C. |
D. |
已知 , 由如右程序框图输出的
, 由如右程序框图输出的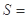 ( )
( )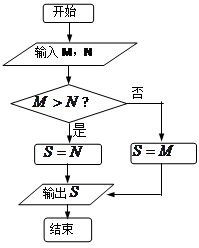
A. |
B. |
C. |
D. |
设函数 的图像关于直线
的图像关于直线 对称,它的周期是
对称,它的周期是 ,则( )
,则( )
A. 的图象过点 的图象过点 |
B. 在 在 上是减函数 上是减函数 |
C. 的一个对称中心是 的一个对称中心是 |
D.将 的图象向右平移 的图象向右平移 个单位得到函数 个单位得到函数 的图象 的图象 |
点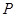 为双曲线
为双曲线 :
: 和圆
和圆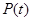 :
: 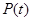 的一个交点,且
的一个交点,且 ,其 中
,其 中 为双曲线
为双曲线 的两个焦点,则双曲线
的两个焦点,则双曲线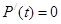 的离心率为
的离心率为
A. |
B. |
C.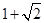 |
D. |
函数 为定义在
为定义在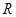 上的减函数,函数
上的减函数,函数 的图像关于点(1,0)
的图像关于点(1,0)
对称, 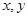 满足不等式
满足不等式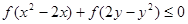 ,
,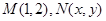 ,
, 为坐标原点,则当
为坐标原点,则当 时,
时, 的取值范围为 ( )
的取值范围为 ( )
A.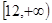 |
B. |
C. |
D.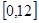 |
点P是曲线 上任一点,则点P到直线
上任一点,则点P到直线 的最小距离为
的最小距离为
在矩形ABCD中,AB=2,BC=1,E为BC的中点,若F为该矩形内(含边界)任意一点,则: 的最大值为______:
的最大值为______:
给出以下命题:
① 双曲线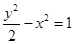 的渐近线方程为
的渐近线方程为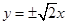 ;
;
② 命题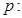 “
“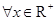 ,
,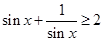 ”是真命题;
”是真命题;
③ 已知线性回归方程为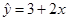 ,当变量
,当变量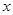 增加
增加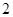 个单位,其预报值平均增加
个单位,其预报值平均增加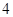 个单位;
个单位;
④ 设随机变量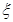 服从正态分布
服从正态分布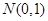 ,若
,若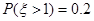 ,则
,则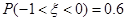 ;
;
⑤ 已知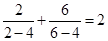 ,
,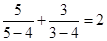 ,
,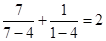 ,
,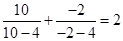 ,依照以上各式的规律,得到一般性的等式为
,依照以上各式的规律,得到一般性的等式为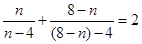 ,(
,( )
)
则正确命题的序号为 (写出所有正确命题的序号).
曲线 与曲线
与曲线 的交点间距离为
的交点间距离为
如图△ABC的外角平分线AD交外接圆于D, ,则
,则

关于 的不等式
的不等式 的解集为空集,则实数
的解集为空集,则实数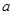 的取值范围为__
的取值范围为__
如图,在△ 中,
中, ,
, 为
为 中点,
中点, .记锐角
.记锐角 .且满足
.且满足 .
.
(1)求 ;
;
(2)求 边上高的值.
边上高的值.
现有长分别为 、
、 、
、 的钢管各
的钢管各 根(每根钢管质地均匀、粗细相同且附有不同的编号),从中随机抽取
根(每根钢管质地均匀、粗细相同且附有不同的编号),从中随机抽取 根(假设各钢管被抽取的可能性是均等的,
根(假设各钢管被抽取的可能性是均等的, ),再将抽取的钢管相接焊成笔直的一根.
),再将抽取的钢管相接焊成笔直的一根.
(1)当 时,记事件
时,记事件 {抽取的
{抽取的 根钢管中恰有
根钢管中恰有 根长度相等},求
根长度相等},求 ;
;
(2)当 时,若用
时,若用 表示新焊成的钢管的长度(焊接误差不计),①求
表示新焊成的钢管的长度(焊接误差不计),①求 的分布列;
的分布列;
②令 ,
, ,求实数
,求实数 的取值范围.
的取值范围.
如图,四边形PCBM是直角梯形, ,
, ∥
∥ ,
, .又
.又 ,
, ,直线AM与直线PC所成的角为
,直线AM与直线PC所成的角为 .
.
(1)求证: ;
;
(2)求二面角 的余弦值.
的余弦值.
已知函数
 .
.
(1)若 为
为 的极值点,求实数
的极值点,求实数 的值;
的值;
(2)当 时,方程
时,方程 有实根,求实数
有实根,求实数 的最大值。
的最大值。
已知抛物线和椭圆都经过点 ,它们在
,它们在 轴上有共同焦点,椭圆的对称轴是坐标轴,抛物线的顶点为坐标原点.
轴上有共同焦点,椭圆的对称轴是坐标轴,抛物线的顶点为坐标原点.
(1)求这两条曲线的方程;
(2)对于抛物线上任意一点 ,点
,点 都满足
都满足 ,求
,求 的取值范围.
的取值范围.
已知正项数列 的前
的前 项和为
项和为 ,且
,且
 .
.
(1)求 的值及数列
的值及数列 的通项公式;
的通项公式;
(2)求证:
 ;
;
(3)是否存在非零整数 ,使不等式
,使不等式
对一切 都成立?若存在,求出
都成立?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.