函数 的最小正周期是_____________
的最小正周期是_____________
在 的二项展开式中,常数项是
的二项展开式中,常数项是
已知正数 、
、 满足
满足 ,则
,则 的最小值是
的最小值是
执行如图所示的程序框图,输出的 值为
值为 
已知直线 与函数
与函数 及函数
及函数 的图像分别相交于
的图像分别相交于 、
、 两点,则
两点,则 、
、 两点之间的距离为
两点之间的距离为
用铁皮制作一个无盖的圆锥形容器,已知该圆锥的母线与底面所在的平面所成角为 ,容器的高为10cm,制作该容器需要 cm2的铁皮
,容器的高为10cm,制作该容器需要 cm2的铁皮
若实数t满足f(t)=-t,则称t是函数f(x)的一个次不动点.设函数 与反函数的所有次不动点之和为m,则m=______
与反函数的所有次不动点之和为m,则m=______
关于 的方程
的方程
 的一个根是
的一个根是
 ,在复平面上的一点
,在复平面上的一点 对应的复数
对应的复数 满足
满足 ,则
,则 的取值范围是
的取值范围是
在极坐标系中,直线 的位置关系是 _
的位置关系是 _
已知函数 ,且
,且 ,则不等式
,则不等式 的解集是
的解集是
设 是定义在
是定义在 上以2为周期的偶函数,已知
上以2为周期的偶函数,已知 ,
, ,则函数
,则函数 在
在 上的解析式是
上的解析式是
设正项数列 的前
的前 项和是
项和是 ,若
,若 和{
和{ }都是等差数列,且公差相等,则
}都是等差数列,且公差相等,则
椭圆 上的任意一点
上的任意一点 (除短轴端点除外)与短轴两个端点
(除短轴端点除外)与短轴两个端点 的连线交
的连线交 轴于点
轴于点 和
和 ,则
,则 的最小值是
的最小值是
如图放置的等腰直角三角形ABC薄片(∠ACB=90°,AC=2)沿x轴滚动,设顶点A(x,y)的轨迹方程是y=f(x),当 [0,
[0, ]时y=f(x)= _____________
]时y=f(x)= _____________
下列命题中正确的是( )
A.函数 与 与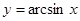 互为反函数 互为反函数 |
B.函数 与 与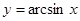 都是增函数 都是增函数 |
C.函数 与 与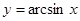 都是奇函数 都是奇函数 |
D.函数 与 与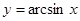 都是周期函数 都是周期函数 |
设事件 ,
, ,已知
,已知 =
= ,
, =
= ,
, =
= ,则
,则 ,
, 之间的关系一定为( )
之间的关系一定为( )
| A.两个任意事件 | B.互斥事件 | C.非互斥事件 | D.对立事件 |
数列 前
前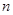 项和为
项和为 ,已知
,已知 ,且对任意正整数
,且对任意正整数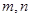 ,都有
,都有 ,若
,若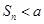 恒成立,则实数
恒成立,则实数 的最小值为( )
的最小值为( )
A.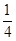 |
B. |
C. |
D.4 |
直线 与双曲线
与双曲线 的渐近线交于
的渐近线交于 两点,设
两点,设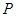 为双曲线
为双曲线 上的任意一点,若
上的任意一点,若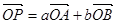 (
( 为坐标原点),则下列不等式恒成立的是( )
为坐标原点),则下列不等式恒成立的是( )
(
A. |
B. |
C. |
D. |
长方体 中,底面
中,底面 是正方形,
是正方形, ,
, 是
是 上的一点.
上的一点.
⑴求异面直线 与
与 所成的角;
所成的角;
⑵若 平面
平面 ,求三棱锥
,求三棱锥 的体积;
的体积;
位于A处的雷达观测站,发现其北偏东45°,与 相距20
相距20 海里的B处有一货船正以匀速直线 行驶,20分钟后又测得该船只位于观测站A北偏东
海里的B处有一货船正以匀速直线 行驶,20分钟后又测得该船只位于观测站A北偏东
 的C处,
的C处, .在离观测站A的正南方某处E,
.在离观测站A的正南方某处E,

(1)求 ; (2)求该船的行驶速度v(海里/小时);
; (2)求该船的行驶速度v(海里/小时);
三阶行列式 , 元素
, 元素
 的代数余子式为
的代数余子式为 ,
, ,
,
(1) 求集合 ;
;
(2)函数 的定义域为
的定义域为 若
若 求实数
求实数 的取值范围;
的取值范围;
已知数列{an}中,a2=1,前n项和为Sn,且 .
.
(1)求a1,a3;
(2)求证:数列{an}为等差数列,并写出其通项公式;
(3)设 ,试问是否存在正整数p,q(其中1<p<q),使b1,bp,bq成等比数列?若存在,求出所有满足条件的数组(p,q);若不存在,说明理由.
,试问是否存在正整数p,q(其中1<p<q),使b1,bp,bq成等比数列?若存在,求出所有满足条件的数组(p,q);若不存在,说明理由.
动圆 过定点
过定点
 ,且与直线
,且与直线 相切,其中
相切,其中 .设圆心
.设圆心 的轨迹
的轨迹 的程为
的程为
(1)求 ;
;
(2)曲线 上的一定点
上的一定点 (
(
 0) ,方向向量
0) ,方向向量 的直线
的直线 (不过P点)与曲线
(不过P点)与曲线 交与A、B两点,设直线PA、PB斜率分别为
交与A、B两点,设直线PA、PB斜率分别为 ,
, ,计算
,计算 ;
;
(3)曲线 上的两个定点
上的两个定点 、
、 ,分别过点
,分别过点 作倾斜角互补的两条直线
作倾斜角互补的两条直线 分别与曲线
分别与曲线 交于
交于 两点,求证直线
两点,求证直线 的斜率为定值;
的斜率为定值;