已知全集
，集合
，则
若复数
满足
（
是虚数单位），则
已知直线
的倾斜角大小是
，则
若关于
的二元一次方程组
有唯一一组解，则实数
的取值范围是
已知函数
和函数
的图像关于直线
对称，
则函数的解析式为
已知双曲线的方程为
，则此双曲线的焦点到渐近线的距离为
函数
的最小正周期
若
展开式中含
项的系数等于含
项系数的8倍，则正整数
执行如图所示的程序框图，若输入
的值是
，则输出
的值是 
已知圆锥底面半径与球的半径都是
，如果圆锥的体积恰好也与球的体积相等，那么这个圆锥的母线长为 
．
某中学在高一年级开设了
门选修课，每名学生必须参加这门选修课中的一门，对于该年级的甲、乙、丙
名学生，这名学生选择的选修课互不相同的概率是 (结果用最简分数表示)．
各项为正数的无穷等比数列
的前
项和为
，若
， 则其公比
的取值范围是.
已知两个不相等的平面向量
，
(
)满足||＝2，且与－的夹角为120°，则|
|的最大值是
给出30行30列的数表
：
，其特点是每行每列都构成等差数列，记数表主对角线上的数
按顺序构成数列
，存在正整数
使
成等差数列，试写出一组
的值
已知
，
，则
的值等于 （ ）
A． ． |
B． ． |
C． ． |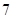
D． ． |
已知圆
的极坐标方程为
，则“
”是“圆与极轴所在直线相切”的 （ ）
| A．充分不必要条件． | B．必要不充分条件． |
| C．充要条件． | D．既不充分又不必要条件． |
若直线
经过点
，则 （ ）
A． ． |
B． ． |
C． ． |
D． ． |
已知集合
，若对于任意
，存在
， 使得
成立，则称集合
是“
集合”. 给出下列4个集合：
① 
② 
③ 
④ 
其中所有“集合”的序号是 （ ）
| A．②③ ． | B．③④ ． | C．①②④． | D．①③④． |
在棱长为
的正方体
中，
分别为
的中点．
（1）求直线
与平面
所 成 角的大小；
（2）求二面角
的大小．
如图所示，扇形
，圆心角的大小等于
，半径为
，在半径
上有一动点
，过点作平行于
的直线交弧
于点
．
（1）若是半径的中点，求线段
的大小；
（2）设
，求△
面积的最大值及此时
的值．
已知函数
．
（1）若
是偶函数，在定义域上
恒成立，求实数
的取值范围；
（2）当
时，令
，问是否存在实数
，使
在
上是减函数，在
上是增函数？如果存在，求出的值；如果不存在，请说明理由．
已知点
，
、
、
是平面直角坐标系上的三点，且
、
、
成等差数列，公差为
，
．
（1）若坐标为
，
，点在直线
上时，求点的坐标；
（2）已知圆
的方程是
，过点
的直线交圆于
两点，
是圆上另外一点，求实数的取值范围；
（3）若、、都在抛物线
上，点的横坐标为
，求证：线段
的垂直平分线与
轴的交点为一定点，并求该定点的坐标．
已知数列
的前
项和为
，且满足
(
)，
，设
，
．
（1）求证：数列
是等比数列；
（2）若
≥
，，求实数
的最小值；
（3）当
时，给出一个新数列
，其中
，设这个新数列的前项和为
，若可以写成
(
且
)的形式，则称为“指数型和”．问
中的项是否存在“指数型和”，若存在，求出所有“指数型和”；若不存在，请说明理由．