下列方程中是一元一次方程的是( )
| A．2x=3y | B．7x+5=6(x-1) |
| C．x2-0.5x=2 | D． |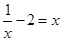
方程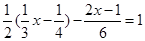
变形正确的是( )
A． |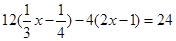
B． |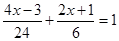
C． |
D． |
若
是方程
的解，则a的值是( )
| A．5 | B．2 | C．1 | D．-5 |
用代入法解方程组
代入后化简比较容易的变形是 ( )
A．由①得 |
B．由①得 |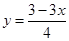
C．由②得 |
D．由②得 |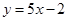
如果不等式
的解集为x＜1，则( )
| A．a≠1 | B．a＞1 | C．a＜1 | D．a为任意有理数 |
下列不等式中，是一元一次不等式组的有（ ）
①
②
③
④
⑤
| A．5个 | B．4个 | C．3个 | D．2个 |
若关于x的方程
和方程
的解互为相反数，则m的值为（ ）
A． |
B． |
C．0 | D．-2 |
现有鸡、兔同笼，已知鸡与兔头数之和为100，鸡与兔之脚数之和为360，设鸡有x只，所列方程是（ ）
A． |
B． |
C． |
D． |
若
，则x的值等于( )
| A．-1 | B．1 | C．2 | D．-2 |
若不等式组
有解，则a的取值范围是（ ）
A． |
B． |
C． |
D． |
若关于x的不等式
的解集为
，则m等于（ ）
| A．1 | B．2 | C．3 | D．4 |
方程
的一组正整数解是（ ）
A． |
B． |
C． |
D． |
已知方程
，用含x的代数式表示y的式子是 。
一个两位数，它的十位数字与个位数字之和为6，则符合条件的数有 个。
若
是关于x的一元一次方程，则m= 。
定义运算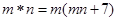
，则式子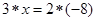
中的x= 。
若不等式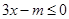
的正整数解是1、2，则m的取值范围是 。
解方程组
得到的x、y的值都不大于1，则m的取值范围是 。
解下列方程：①
；②
解下列方程组：①
；②
解下列不等式（组），并把解集在数轴上表示出来：
①
；②
当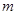
为何值时，关于x的方程
的解是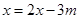
的解的2倍。
客车和货车分别在两条平行的铁轨上行驶，客车长450米，货车长600米。如果两车相向而行，那么从两车车头相遇到车尾离开共需21秒钟；如果客车从后面追货车，那么客车车头追上货车车尾到客车车尾离开货车车头共需1分45秒。求两车速度。
若不等式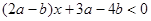
的解集是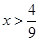
，求不等式
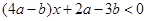的解集。
某家电商场计划用9万元从生产厂家购进50台电视机．已知该厂家生产3种不同型号的电视机，出厂价分别为A种每台1500元，B种每台2100元，C种每台2500元．
（1）若家电商场同时购进两种不同型号的电视机共50台，用去9万元，请你研究一下商场的进货方案；
（2）若商场销售一台A种电视机可获利150元，销售一台B种电视机可获利200元，销售一台C种电视机可获利250元，在同时购进两种不同型号的电视机方案中，为了使销售时获利最多，你选择哪种方案？
有三块牧场，草长得一样密一样快，面积分别为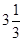
公顷，10公顷和24公顷，第一块12头牛可吃4星期，第二块21头牛可吃9星期，第三块可供多少头牛吃18个星期？