由“半径为R的圆内接矩形中,正方形的面积最大”,推理出“半径为R的球的内接长方体中,正方体的体积最大”是( )
| A.归纳推理 | B.类比推理 | C.演绎推理 | D.以上都不是 |
有一段演绎推理是这样的“有些有理数是真分数,整数是有理数,则整数是真分数”该结论显然是错误的,其原因是
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.非以上错误 |
函数 的导数是( )
的导数是( )
A.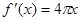 |
B.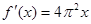 |
C.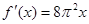 |
D.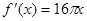 |
复数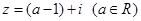 是纯虚数,则
是纯虚数,则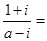 ( )
( )
A.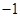 |
B.1 | C.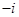 |
D.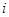 |
在用数学归纳法证明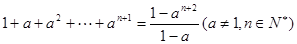 时,在验证当
时,在验证当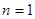 时,等式左边为( )
时,等式左边为( )
| A.1 | B.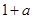 |
C.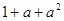 |
D.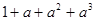 |
已知函数 的图象如图,则
的图象如图,则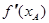 与
与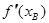 的大小关系是( )
的大小关系是( ) 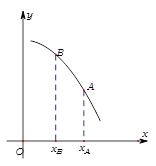
A.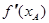 > >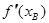 |
B.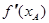 < <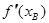 |
C.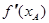 = =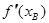 |
| D.不能确定 |
已知函数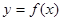 ,其导函数
,其导函数 的图象如图所示,则
的图象如图所示,则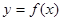 ( )
( )
| A.在(-∞,0)上为减函数 | B.在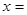 0处取极小值 0处取极小值 |
| C.在(4,+∞)上为减函数 | D.在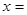 2处取极大值 2处取极大值 |
曲线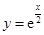 在点
在点 处的切线与坐标轴所围三角形的面积为( )
处的切线与坐标轴所围三角形的面积为( )
A.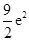 |
B.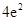 |
C.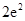 |
D.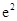 |
已知数列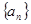 满足
满足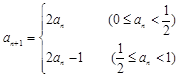 若
若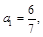 则
则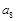 的值为( )
的值为( )
A.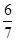 |
B.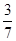 |
C.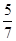 |
D.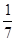 |
已知函数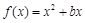 的图象在点
的图象在点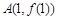 处的切线的斜率为3,数列
处的切线的斜率为3,数列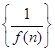 的前
的前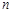 项和为
项和为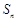 ,则
,则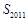 的值为( )
的值为( )
A.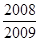 |
B. |
C.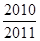 |
D.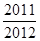 |
设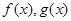 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当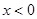 时,
时,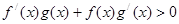 ,且
,且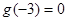 ,则
,则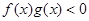 的解集是( )
的解集是( )
| A.(-3,0)∪(3,+∞) | B.(-3,0)∪(0,3) |
| C.(-∞,-3)∪(3,+∞) | D. (-∞,-3)∪(0,3) |
若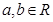 ,
,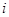 是虚数单位,且
是虚数单位,且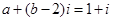 ,则
,则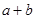 的值为
的值为
观察下列等式: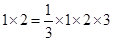 ,
,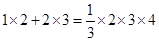 ,
,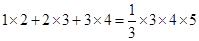 ,…, 照此规律,
,…, 照此规律,
计算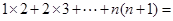 (
(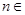 N
N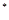 ).
).
已知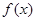 为一次函数,且
为一次函数,且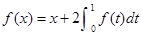 ,则
,则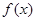 =
=
已知曲线方程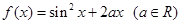 ,若对任意实数
,若对任意实数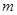 ,直线
,直线
都不是曲线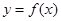 的切线,则
的切线,则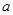 的取值范围是
的取值范围是
已知曲线 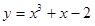 在点
在点 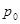 处的切线
处的切线 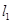 平行直线
平行直线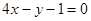 ,且点
,且点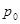 在第三象限.
在第三象限.
(Ⅰ)求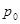 的坐标;
的坐标;
(Ⅱ)若直线 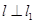 , 且
, 且  也过切点
也过切点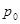 ,求直线
,求直线 的方程.
的方程.
设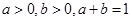 求证:
求证: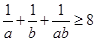
已知a、b、c成等差数列且公差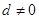 ,求证:
,求证: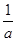 、
、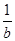 、
、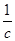 不可能成等差数列
不可能成等差数列
将边长为 米的一块正方形铁皮的四角各截去一个大小相同的小正方形,然后将四边折起做成一个无盖的方盒.欲使所得的方盒有最大容积,截去的小正方形的边长应为多少米?方盒的最大容积为多少?
米的一块正方形铁皮的四角各截去一个大小相同的小正方形,然后将四边折起做成一个无盖的方盒.欲使所得的方盒有最大容积,截去的小正方形的边长应为多少米?方盒的最大容积为多少?
已知数列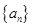 的前
的前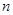 项和为
项和为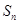 ,且对任意的
,且对任意的 都有
都有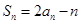 ,
,
(Ⅰ)求数列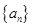 的前三项
的前三项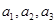 ;
;
(Ⅱ)猜想数列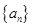 的通项公式
的通项公式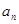 ,并用数学归纳法证明
,并用数学归纳法证明
若存在实常数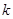 和
和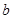 ,使得函数
,使得函数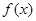 和
和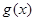 对其定义域上的任意实数
对其定义域上的任意实数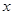 分别满足:
分别满足: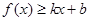 和
和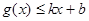 ,则称直线
,则称直线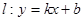 为
为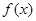 和
和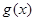 的“隔离直线”.已知
的“隔离直线”.已知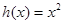 ,
,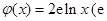 为自然对数的底数).
为自然对数的底数).
(Ⅰ)求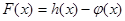 的极值;
的极值;
(Ⅱ)函数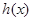 和
和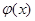 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.