下列命题中正确的是( )
| A.第一象限角必是锐角 | B.终边相同的角相等 |
| C.负角必是第四象限角 | D.相等的角终边必相同 |
 ( )
( )
| A.0 | B.1 | C.2 | D.-2 |
已知 ,
,  , 且
, 且 , 则
, 则 等于 ( )
等于 ( )
A -1 B -9 C 9 D 1
已知 ,则
,则 化简的结果为 ( )
化简的结果为 ( )
A.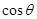 |
B.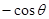 |
C. |
D.以上都不对 |
下列各组向量中,可以作为基底的是 ( )
A. |
B.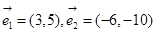 |
C.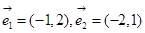 |
D. |
设函数f(x)=sin(2x- ),xÎR,则f(x)是( )
),xÎR,则f(x)是( )
| A.最小正周期为p的奇函数 | B.最小正周期为p的偶函数 |
C.最小正周期为 的奇函数 的奇函数 |
D.最小正周期为 的偶函数 的偶函数 |
在边长为 的正三角形ABC中,设
的正三角形ABC中,设 ,则
,则 等于( )
等于( )
| A.0 | B.1 | C.3 | D.-3 |
若 是△
是△ 的一个内角,且
的一个内角,且 ,则
,则 的值为( )
的值为( )
A. |
B. |
C. |
D. |
在四边形ABCD中,若 ,且
,且 ,则( )
,则( )
| A.ABCD是矩形 | B.ABCD是正方形 |
| C.ABCD是菱形 | D.ABCD是平行四边形 |
要得到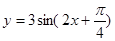 的图象只需将
的图象只需将 的图象 ( )
的图象 ( )
A.向左平移 个单位 个单位 |
B.向右平移 个单位 个单位 |
C.向左平移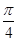 个单位 个单位 |
D.向右平移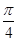 个单位 个单位 |
函数 在一个周期内的图象如右,则此函数的解析式为( )
在一个周期内的图象如右,则此函数的解析式为( )
A. |
B. |
C. |
D. |
设扇形的周长为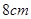 ,面积为
,面积为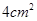 ,则扇形的圆心角的弧度数是 。
,则扇形的圆心角的弧度数是 。
已知 ,
, ,若
,若 平行,则λ= .
平行,则λ= .
如图所示,向量 ,
, 在一条直线上,且
在一条直线上,且 ,则
,则 __________________(用
__________________(用 表示)
表示)
关于函数f(x)=4sin(2x+ ), (x∈R)有下列命题:
), (x∈R)有下列命题:
①f(x)是以2π为最小正周期的周期函数;
②f(x)可改写为y=4cos(2x- );
);
③f(x)的图象关于点(- ,0)对称;
,0)对称;
④f(x)的图象关于直线x=- 对称;
对称;
其中正确的序号为 。
已知 ,
,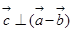 。
。
(1)求 ,
,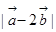 ;(2)若
;(2)若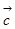 为单位向量,求
为单位向量,求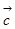 的坐标。
的坐标。
已知 ,计算:
,计算:
(1) (2)
(2)
已知 ,
,
(1)求 与
与 的夹角
的夹角 ; (2)求
; (2)求 。
。
已知 ,
, 。
。
(1)求 的振幅,最小正周期,对称轴,对称中心。
的振幅,最小正周期,对称轴,对称中心。
(2)说明 是由余弦曲线经过怎样变换得到。
是由余弦曲线经过怎样变换得到。
已知 ,
, ,
, ,
, .
.
(1)若 (
( 为坐标原点),求
为坐标原点),求 与
与 的夹角;
的夹角;
(2)若 ,求
,求 的值.
的值.
已知函数 (
( ),该函数所表示的曲线上的一个最高点为
),该函数所表示的曲线上的一个最高点为 ,由此最高点到相邻的最低点间曲线与x轴交于点(6,0)。
,由此最高点到相邻的最低点间曲线与x轴交于点(6,0)。
(1)求 函数解析式;
函数解析式;
(2)求函数 的单调区间;
的单调区间;
(3)若 ,求
,求 的值域。
的值域。