设 ,
, ,则有( ).
,则有( ).
A. |
B. |
C. |
D. |
关于复数的命题:
(1)复数 ;(2)复数
;(2)复数 的模为
的模为 ;
;
(3)在复平面内,纯虚数与 轴上的点一一对应,其中真命题的个数是( ).
轴上的点一一对应,其中真命题的个数是( ).
| A.0个 | B.1个 | C.2个 | D.3个 |
一个简单几何体的主视图,左视图如图所示,则其俯视图不可能为( ) .
| A.长方形 |
| B.直角三角形 |
| C.圆 |
| D.椭圆 |
甲、乙两名运动员在某项测试中的6次成绩的茎叶图如图所示, ,
, 分别表示甲乙两名运动员这项测试成绩的平均数,
分别表示甲乙两名运动员这项测试成绩的平均数, 分别表示甲乙两名运动员这项测试成绩的标准差,则有( ).
分别表示甲乙两名运动员这项测试成绩的标准差,则有( ).
A. |
B. |
C. |
D. |
设 是直线,
是直线, ,
, 是两个不同的平面,下列命题正确的是( ).
是两个不同的平面,下列命题正确的是( ).
A.若 , , ,则 ,则 |
B.若 , , ,则 ,则 |
C.若 , , ,则 ,则 |
D.若 , ,  ,则 ,则 |
函数 的值域为( ).
的值域为( ).
| A.[-2 ,2] | B.[- , , ] ] |
C.[-1,1] | D.[- , ,  ] ] |
公差不为零的等差数列 的前
的前 项和为
项和为 ,若
,若 是
是 与
与 的等比中项,且
的等比中项,且 ,则
,则 =( )
=( )
| A.80 | B.160 | C.320 | D.640 |
定义在 上的函数
上的函数 ,满足
,满足 ,
, ,若
,若 且
且 ,则有( ).
,则有( ).
A. |
B. |
C. |
D.不能确定 |
设 ,
, 是双曲线
是双曲线 的左右两个焦点,若在双曲线的右支上存在一点
的左右两个焦点,若在双曲线的右支上存在一点 ,使
,使 (
( 为原点)且
为原点)且 ,则双曲线的离心率为( ).
,则双曲线的离心率为( ).
A. |
B. |
C. |
D. |
如图,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕着C旋转后与点B绕点P旋转后重合于点D,设CP=x,△CPD的面积为f(x).求f(x)的最大值( ).
A. |
B.2 |
| C.3 | D. |
已知向量 则
则 的最大值为 .
的最大值为 .
下列程序框图输出的结果 ,
, .
.
在二项式 的展开式中,含
的展开式中,含 的项的系数是 .
的项的系数是 .
如图,将正 分割成16个全等的小正三角形,在每个三角形的顶点各放置一个数,使位于同一直线上的点放置的数(当数的个数不少于3时)都分别依次成等差数列,若顶点
分割成16个全等的小正三角形,在每个三角形的顶点各放置一个数,使位于同一直线上的点放置的数(当数的个数不少于3时)都分别依次成等差数列,若顶点 处的三个数互不相同且和为1,则所有顶点的数之和
处的三个数互不相同且和为1,则所有顶点的数之和 .
.
(1)设点 的极坐标为
的极坐标为 ,直线
,直线 过点
过点 且与极轴垂直,则直线
且与极轴垂直,则直线 的极坐标方程为 .
的极坐标方程为 .
(2)已知函数 ,若关于
,若关于 的不等式
的不等式 的解集为
的解集为 ,则
,则 的取值范围是 .
的取值范围是 .
已知 的内角
的内角 所对边分别为
所对边分别为 ,且
,且 .
.
(1)求角 的大小;
的大小;
(2)若 ,求边长
,求边长 的最小值.
的最小值.
已知直角梯形 中,
中, ,
, ,
, ,
, 是等边三角形,平面
是等边三角形,平面 ⊥平面
⊥平面 .
.
(1)求二面角 的余弦值;
的余弦值;
(2)求 到平面
到平面 的距离.
的距离.
某医院将一专家门诊已诊的1000例病人的病情及诊断所用时间(单位:分钟)进行了统计,如下表.若视频率为概率,请用有关知识解决下列问题.
| 病症及代号 |
普通病症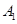 |
复诊病症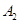 |
常见病症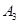 |
疑难病症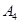 |
特殊病症 |
| 人数 |
100 |
300 |
200 |
300 |
100 |
| 每人就诊时间(单位:分钟) |
3 |
4 |
5 |
6 |
7 |
用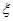 表示某病人诊断所需时间,求
表示某病人诊断所需时间,求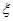 的数学期望.
的数学期望.
并以此估计专家一上午(按3小时计算)可诊断多少病人;
某病人按序号排在第三号就诊,设他等待的时间为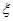 ,求
,求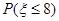 ;
;
求专家诊断完三个病人恰好用了一刻钟的概率.
已知 是数列
是数列 的前
的前 项和,且对任意
项和,且对任意 ,有
,有 ,
,
求 的通项公式;
的通项公式;
求数列 的前
的前 项和
项和 .
.
设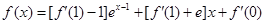
求 及
及 的单调区间
的单调区间
设 ,
,
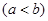 两点连线的斜率为
两点连线的斜率为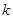 ,问是否存在常数
,问是否存在常数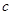 ,且
,且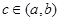 ,当
,当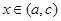 时有
时有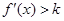 ,当
,当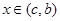 时有
时有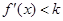 ;若存在,求出
;若存在,求出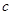 ,并证明之,若不存在说明理由.
,并证明之,若不存在说明理由.