设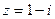 (
(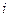 为虚数单位),则
为虚数单位),则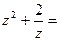
A.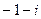 |
B.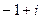 |
C.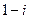 |
D.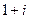 |
若集合 那么M∩N=
那么M∩N=
A.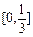 |
B.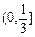 |
C.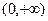 |
D.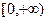 |
设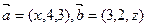 ,且
,且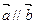 ,则
,则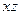 等于
等于
A. |
B.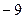 |
C.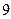 |
D.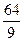 |
已知函数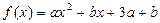 是定义域为
是定义域为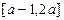 的偶函数,则
的偶函数,则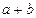 的值
的值
| A.0 | B. |
C.1 | D.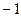 |
对于定义在R上的奇函数 ,满足
,满足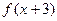 =
= ,若
,若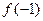 =1,则
=1,则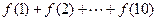 =
=
| A.0 | B.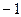 |
C.1 | D.10 |
对于大于1的自然数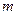 的
的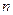 次幂可用奇数进行如图所示的“分裂”,仿此,记
次幂可用奇数进行如图所示的“分裂”,仿此,记 的“分裂”中的最小数为
的“分裂”中的最小数为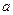 ,而
,而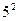 的“分裂”中最大的数是
的“分裂”中最大的数是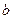 ,则
,则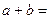
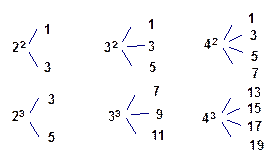
| A.30 | B.26 |
| C.32 | D.36 |
若函数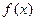 在R上可导,且
在R上可导,且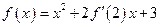 ,则
,则
A.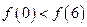 |
B.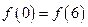 |
C.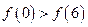 |
D.无法确定 |
函数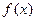 在定义域
在定义域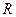 内可导,若
内可导,若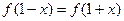 ,且当
,且当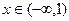 时,
时,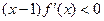 ,设
,设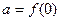 ,
,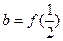 ,
, ,则
,则
A.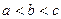 |
B.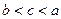 |
C.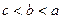 |
D.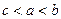 |
若关于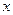 的不等式
的不等式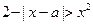 至少有一个负数解,则实数
至少有一个负数解,则实数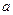 的取值范围是
的取值范围是
A.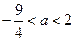 |
B.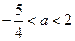 |
C.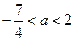 |
D.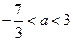 |
已知函数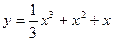 的图象C上存在一点P满足:若过点P的直线
的图象C上存在一点P满足:若过点P的直线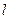 与曲线C交于不同于P的两点M(
与曲线C交于不同于P的两点M(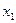 ,
,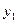 )、N
)、N (
(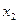 ,
,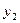 ),恒
),恒 有
有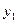 +
+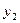 为
为 定值
定值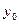 ,则
,则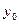 的值为
的值为
A.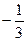 |
B.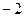 |
C.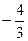 |
D.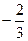 |
如果复数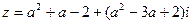 为纯虚数,那么实数a的值为 ▲
为纯虚数,那么实数a的值为 ▲
曲线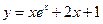 在点(0,1)处的切线方程为 ▲
在点(0,1)处的切线方程为 ▲
函数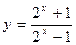 的值域是 ▲
的值域是 ▲
已知平行六面体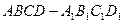 中
中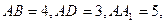
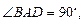
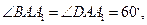 则
则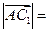 ▲
▲
已知函数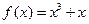 (
(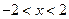 ),则不等式
),则不等式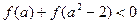 的解集为 ▲
的解集为 ▲
在解决问题:“证明数集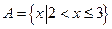 没有最小数”时,可用反证法证明.
没有最小数”时,可用反证法证明.
假设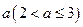 是
是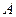 中的最小数,则取
中的最小数,则取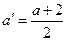 ,可得:
,可得: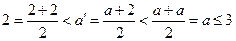 ,与假设中“
,与假设中“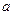 是
是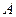 中的最小数”矛盾!那么对于问题:“证明数集
中的最小数”矛盾!那么对于问题:“证明数集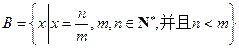 没有最大数”,也可以用反证法证明.我们可以假设
没有最大数”,也可以用反证法证明.我们可以假设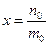 是
是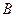 中的最大数,则可以找到
中的最大数,则可以找到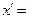 ▲ (用
▲ (用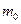 ,
,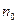 表示),由此可知
表示),由此可知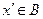 ,
,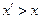 ,这与假设矛盾!所以数集
,这与假设矛盾!所以数集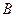 没有最大数.
没有最大数.
已知函数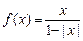 ,分别给出下面几个结论:
,分别给出下面几个结论:
①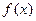 是奇函数; ②函数
是奇函数; ②函数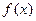 的值域为R;
的值域为R;
③若x1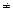 x2,则一定有
x2,则一定有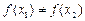 ;④函数
;④函数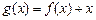 有三个零点.
有三个零点.
其中正确结论的序号有 ▲ .(请将你认为正确的结论的序号都填上)
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,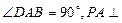 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC=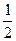 AB=1,M是PB的中点。
AB=1,M是PB的中点。
(1)求直线AC与PB所成角的余弦值;
(2)求面AMC与面PMC所成锐二面角的大小的余弦值。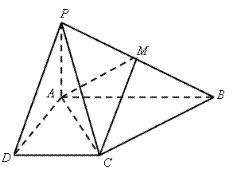
数列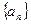 满足
满足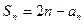 ,其中
,其中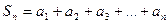 ,求
,求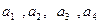 值,猜想
值,猜想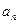 ,并用数学归纳法加以证明。
,并用数学归纳法加以证明。
已知函数 ,常数
,常数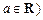
(1)讨论函数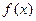 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)若函数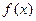 在
在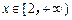 上为增函数,求
上为增函数,求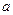 的取值范围.
的取值范围.
设函数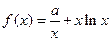
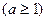 ,
,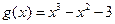 .
.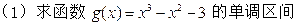 ;
;
(2)如果存在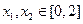 ,使得
,使得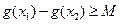 ,求满足上述条件的最大整数
,求满足上述条件的最大整数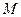 ;
;
(3)求证:对任意的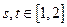 ,都有
,都有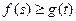 成立.
成立.
(请考生在下面甲、乙两题中任选一题做答,如果多做,则按所做的甲题计分)
甲题:
(1)若关于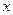 的不等式
的不等式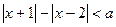 的解集不是空集,求实数
的解集不是空集,求实数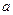 的取值范围;
的取值范围;
(2)已知实数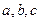 ,满足
,满足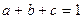 ,求
,求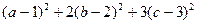 最小值.
最小值.
乙题:
已知曲线C的极坐标方程是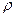 =4cos
=4cos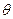 。以极点为平面直角坐标系的原点,极轴为
。以极点为平面直角坐标系的原点,极轴为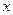 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线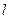 的参数方程是
的参数方程是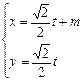 (
(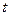 是参数)。
是参数)。
(1)将曲线C的极坐标方程化成直角坐标方程并把直线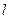 的参数方程转化为普通方程;
的参数方程转化为普通方程;
(2)若过定点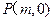 的直线
的直线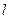 与曲线C相交于A、B两点,且
与曲线C相交于A、B两点,且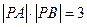 ,试求实数
,试求实数 的值。
的值。