设集合 ,则
,则 中元素的个数为( )
中元素的个数为( )
| A.1个 | B.2个 | C.3个 | D.大于3个 |
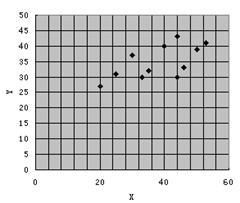
某次数学测试分为选择题与非选择题两部分,
右边的散点图中每个点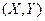 表示一位学生在
表示一位学生在
这两部分的得分,其中 表示该生选择题得
表示该生选择题得
分, 表示该生非选择题得分,设
表示该生非选择题得分,设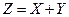 表
表
示该生的总分,现有11位学生的得分数据,根
据散点图,下列判断正确的是( )
A. 的方差< 的方差< 的方差 的方差 |
B. 的中位数> 的中位数> 的中位数 的中位数 |
C. 的众数< 的众数< 的众数 的众数 |
D.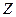 的中位数= 的中位数= 的中位数+ 的中位数+ 的中位数 的中位数 |
已知 表示不超过x的最大整数,如
表示不超过x的最大整数,如 ,若
,若 是方程
是方程 的实数根,则( )
的实数根,则( )
A. |
B. |
C. |
D. |
已知函数 的图象与直线
的图象与直线 的三个相邻交点的横坐标分别是2,4,8,则
的三个相邻交点的横坐标分别是2,4,8,则 的单调递减区间是( )
的单调递减区间是( )
A. |
B. |
C. |
D. |
若映射 ,满足:
,满足: 且
且 ,那么
,那么 的值为( )
的值为( )
A. |
B. |
C. |
D. |
已知四边形 ,
, 是
是 的垂直平分线,垂足
的垂直平分线,垂足
为 ,
, 为直线
为直线 外一点.设向量
外一点.设向量 ,
, ,
,
则 的值是( )
的值是( )
A. |
B. |
C. |
D. |
 |
 是一个常数,函数
是一个常数,函数 的值域不可能是( )
的值域不可能是( )
A. |
B. |
C. |
D. |
若 ,
, ,则
,则 的大小关系为( )
的大小关系为( )
A. |
B. |
C. |
D. |
求: =
=
A. |
B. |
C. |
D. |
若函数 有两个不同的零点
有两个不同的零点 ,
, ,那么在
,那么在 两个函数值中( )
两个函数值中( )
A.只有一个小于 |
B.至少有一个小于 |
C.都小于 |
D.可能都大于 |
已知集合 ,
, ,若
,若 ,则实数
,则实数 的取值范围是
的取值范围是
设 ,则
,则 .
.
如图执行右面的程序框图,那么输出的 值为 .
值为 .
 |
在标有数字 的12张大小相同的卡片中,
的12张大小相同的卡片中,
依次取出不同的三张卡片它们的数字和恰好是3的倍数
的概率是 .
在平面直角坐标系中, 为坐标原点,设向量
为坐标原点,设向量 ,
, ,若
,若 且
且 ,
,
则点 所有可能的位置所构成的区域面积是 .
所有可能的位置所构成的区域面积是 .
某学生对函数 的性质进行研究,得出如下的结论:
的性质进行研究,得出如下的结论:
①函数 在
在 上单调递增,在
上单调递增,在 上单调递减;
上单调递减;
②点 是函数
是函数 图像的一个对称中心;
图像的一个对称中心;
③函数 图像关于直线
图像关于直线 对称;
对称;
④存在常数 ,使
,使 对一切实数
对一切实数 均成立.其中正确的结论是 .
均成立.其中正确的结论是 .
已知数据 的平均数为
的平均数为 ,标准差为
,标准差为 ,则数据
,则数据 的平均数的
的平均数的
取值范围是 .
已知向量 ,设函数
,设函数 ,
,
(1)求 的单调区间;
的单调区间;
(2)若 在区间
在区间 上有两个不同的根
上有两个不同的根 ,求
,求 的值.
的值.
已知正实数 ,设
,设 ,
, .
.
(1)当 时,求
时,求 的取值范围;
的取值范围;
(2)若以 为三角形的两边,第三条边长为
为三角形的两边,第三条边长为 构成三角形,求
构成三角形,求 的取值范围.
的取值范围.
设 是定义在实数
是定义在实数 上的函数,
上的函数, 是定义在正整数
是定义在正整数 上的函数,同时满足下列条件:
上的函数,同时满足下列条件:
(1)任意 ,有
,有 ,当
,当 时,
时, 且
且 ;
;
(2) ;
;
(3) ,
,
试求:(1)证明:任意 ,
, ,都有
,都有 ;
;
(2)是否存在正整数 ,使得
,使得 是25的倍数,若存在,求出所有自然数
是25的倍数,若存在,求出所有自然数 ;若不存在说明理由.(阶乘定义:
;若不存在说明理由.(阶乘定义: )
)