函数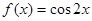 的最小正周期是 .
的最小正周期是 .
直线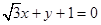 的倾斜角是 .
的倾斜角是 .
复数 的虚部是 .
的虚部是 .
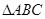 中,“
中,“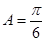 ”是“
”是“ ”的 条件(从“充分不必要”,“必要不充分”,“充要”,“既不充分也不必要”中选出符合题意的一个填空).
”的 条件(从“充分不必要”,“必要不充分”,“充要”,“既不充分也不必要”中选出符合题意的一个填空).
幂函数 过点
过点 ,则
,则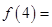 .
.
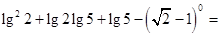 .
.
如果复数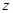 满足
满足 ,那么
,那么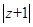 的最大值是 .
的最大值是 .
函数 的单调递增区间是 .
的单调递增区间是 .
圆 ,过点
,过点 的直线
的直线 与圆相交于
与圆相交于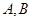 两点,
两点,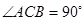 ,则直线
,则直线 的方程是 .
的方程是 .
已知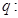 不等式
不等式 对
对 恒成立,若
恒成立,若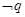 为假,则实数
为假,则实数 的范围是 .
的范围是 .
E,F是等腰直角△ABC斜边BC上的四等分点,则 = .
= .
函数
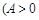 ,
,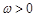 ,
,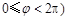 在
在 上的部分图象如图所示,则
上的部分图象如图所示,则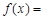 .
. 
已知函数y=f(x)(x∈(0,2))的图象是如图所示的圆C的一段圆弧.现给出如下命题: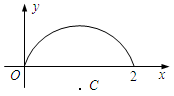
①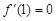 ;②
;② ;③
;③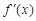 为减函数;④若
为减函数;④若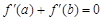 ,则a+b=2.
,则a+b=2.
其中所有正确命题的序号为 .
有 个小球,将它们任意分成两堆,求出这两堆小球球数的乘积,再将其中一堆小球任意分成两堆,求出这两堆小球球数的乘积,如此下去,每次都任选一堆,将这堆小球任意分成两堆,求出这两堆小球球数的乘积,直到不能再分为止,则所有乘积的和为 .
个小球,将它们任意分成两堆,求出这两堆小球球数的乘积,再将其中一堆小球任意分成两堆,求出这两堆小球球数的乘积,如此下去,每次都任选一堆,将这堆小球任意分成两堆,求出这两堆小球球数的乘积,直到不能再分为止,则所有乘积的和为 .
已知集合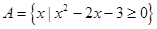 ,
, ,
, .
.
(1)当 时,求
时,求 ;
;
(2)若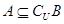 ,求实数
,求实数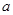 的取值范围.
的取值范围.
已知函数 ,
, .
.
(1)若 ,求证:函数
,求证:函数 是
是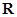 上的奇函数;
上的奇函数;
(2)若函数 在区间
在区间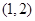 上没有零点,求实数
上没有零点,求实数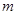 的取值范围.
的取值范围.
在矩形 中,以
中,以 所在直线为
所在直线为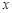 轴,以
轴,以 中点
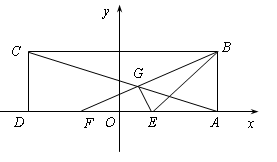
中点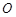 为坐标原点,建立如图所示的平面直角坐标系.已知点
为坐标原点,建立如图所示的平面直角坐标系.已知点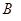 的坐标为
的坐标为 ,E、F为
,E、F为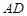 的两个三等分点,
的两个三等分点,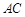 和
和 交于点
交于点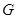 ,
,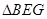 的外接圆为⊙
的外接圆为⊙ .
. 
(1)求证: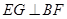 ;
;
(2)求⊙ 的方程;
的方程;
(3)设点 ,过点P作直线与⊙
,过点P作直线与⊙ 交于M,N两点,若点M恰好是线段PN的中点,求实数
交于M,N两点,若点M恰好是线段PN的中点,求实数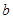 的取值范围.
的取值范围.
已知函数
(1)讨论函数 的单调性;
的单调性;
(2)若 时,关于
时,关于 的方程
的方程 有唯一解,求
有唯一解,求 的值;
的值;
(3)当 时,证明: 对一切
时,证明: 对一切 ,都有
,都有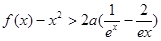 成立.
成立.