已知向量a
 , b
, b
 ,若a⊥b,则实数
,若a⊥b,则实数 的值为
的值为
A. |
B. |
C. |
D. |
2sin75°cos75°的值为
A. |
B. |
C. |
D. |
已知a>b,c>d,且c、d不为0,则下列不等式恒成立的是
A. |
B. |
C. |
D. |
在等差数列 中,
中, ,
, ,则
,则 的前5项和
的前5项和 =
=
| A.7 | B.15 | C.20 | D.25 |
在△ABC中,A=60°,a=,b=,则
| A.B=45°或135° | B.B=135° | C.B=45° | D.以上答案都不对 |
如图阴影部分用二元一次不等式组表示为
A. |
B. |
C. |
D. |
已知 ,
, ,
, ,则
,则 与
与 的夹角是
的夹角是
A.30 |
B.60 |
C.120 |
D.150 |
若 ,则对
,则对 说法正确的是
说法正确的是
A.有最大值 |
B.有最小值 |
| C.无最大值和最小值 | D.无法确定 |
数列{an}的通项公式 (
( ),若前n项的和
),若前n项的和 ,则项数n为
,则项数n为
A. |
B. |
C. |
D. |
函数 (x∈R,
(x∈R, >0,0≤
>0,0≤ <2
<2 的部分图象如下图,则
的部分图象如下图,则
A. = = , , = = |
B. = = , , = = |
C. = = , , = = |
D. = = , , = = |
已知数列 的通项公式
的通项公式 ,则
,则 .
.
如果 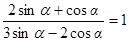 ,那么
,那么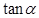 的值为 .
的值为 .
不等式 的解集为 .
的解集为 .
把函数 的图象向左平移
的图象向左平移 个单位长度,再把所得图象上所有点的横坐标伸长到原来的
个单位长度,再把所得图象上所有点的横坐标伸长到原来的 倍(纵坐标不变),所得函数图象的解析式为 .
倍(纵坐标不变),所得函数图象的解析式为 .
已知向量 ,
, .
.
(1)求 和
和 ;
;
(2)当 为何值时,
为何值时, .
.
我舰在敌岛A处南偏西50°的B处,发现敌舰正离开A岛沿北偏西10°的方向以每小时10海里的速度航行,我舰要用2小时的时间追赶敌舰,设图中的 处是我舰追上敌舰的地点,且已知AB距离为12海里.
处是我舰追上敌舰的地点,且已知AB距离为12海里.
(1)求我舰追赶敌舰的速度;
(2)求∠ABC的正弦值.
已知等差数列 的前
的前 项和为
项和为 ,且
,且 ,
,
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和 .
.
已知函数 .
.
(1)求函数 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
(2)若 ,求
,求 的值.
的值.
某公司利用A、B两种原料生产甲、乙两种产品,每生产1吨产品所需要的原料及利润如下表所示:
| |
A种原料(单位:吨) |
B种原料(单位:吨) |
利润(单位:万元) |
| 甲种产品 |
1 |
2 |
3 |
| 乙种产品 |
2 |
1 |
4 |
公司在生产这两种产品的计划中,要求每种产品每天消耗A、B原料都不超过12吨。求每天生产甲、乙两种产品各多少吨,使公司获得总利润最大?最大利润是多少?
已知数列 是首项
是首项 的等比数列,其前
的等比数列,其前 项和
项和 中,
中, 、
、 、
、 成等差数列.
成等差数列.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列{
,求数列{ }的前
}的前 项和为
项和为 ;
;
(3)求满足 的最大正整数
的最大正整数 的值.
的值.