集合 的真子集的个数是
的真子集的个数是
| A.15 | B.14 | C.7 | D.6 |
函数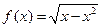 的单调递增区间为
的单调递增区间为
A. |
B.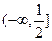 |
C.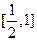 |
D.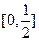 |
若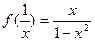 ,则
,则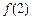 =
=
A.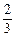 |
B.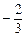 |
C.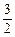 |
D.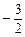 |
若函数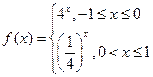 ,则
,则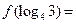
A.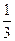 |
B.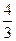 |
C.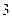 |
D.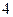 |
已知函数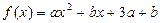 是定义域为
是定义域为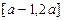 的偶函数,
的偶函数,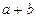 的值是
的值是
| A.0 | B.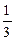 |
C.1 | D.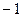 |
对于定义在R上的奇函数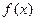 ,满足
,满足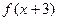 =
=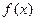 ,若
,若 =1,则
=1,则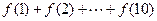 = [
= [
| A.0 | B.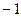 |
C.1 | D.10[ |
若函数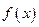 在R上可导,且
在R上可导,且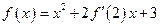 ,则
,则
A.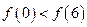 |
B.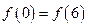 |
C.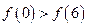 |
D.无法确定 |
函数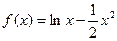 的图象大致是
的图象大致是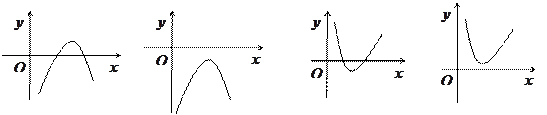
A. B. C. D.
函数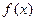 在定义域
在定义域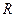 内可导,若
内可导,若 ,且当
,且当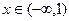 时,
时,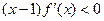 ,设
,设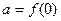 ,
,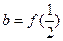 ,
,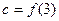 ,则
,则
A.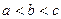 |
B.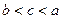 |
C.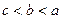 |
D.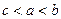 |
已知函数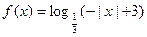 定义域是
定义域是
 ,值域是
,值域是 ,则满足条件的整数对
,则满足条件的整数对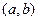 个数有
个数有
| A.3个 | B.4 个 | C.5个 | D.7个 |
设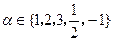 ,则使
,则使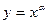 为奇函数且在
为奇函数且在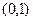 上图象在直线
上图象在直线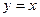 上方的
上方的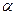 值为 ▲
值为 ▲
已知函数 定义域是[
定义域是[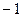 ,2]
,2] ,
,
则函数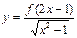 的定义域是 ▲
的定义域是 ▲
函数 的值域是 ▲
的值域是 ▲
曲线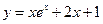 在点(0,1)处的切线方程为 ▲
在点(0,1)处的切线方程为 ▲
设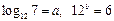 ,则
,则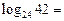 ▲
▲
已知函数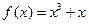 (
(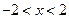 ),则不等式
),则不等式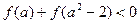 的解集为▲
的解集为▲
已知函数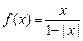 ,分别给出下面几个结论:
,分别给出下面几个结论:
①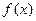 是奇函数; ②函数
是奇函数; ②函数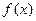 的值域为R;
的值域为R;
③若x1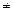 x2,则一定有
x2,则一定有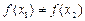 ;④函数
;④函数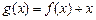 有三个零点.
有三个零点.
其中正确结论的序号有 ▲ .(请将你认为正确的结论的序号都填上)
设全集为R,集合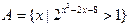 ,
,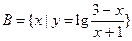 ,
,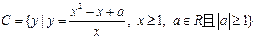
(1)求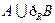 ;(2)若
;(2)若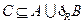 ,求
,求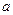 的取值范围
的取值范围
通过研究学生的学习行为,专家发现,学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的兴趣激增;中间有一段时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,设f (t)表示学生注意力随时间t(分钟)的变化规律(f(t)越大,表明学生注意力越集中),经过实验分析得知: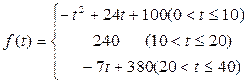
(1)讲课开始后多少分钟,学生的注意力最集中?能持续多少分钟?
(2)讲课开始后5分钟与讲课开始后25分钟比较,何时学生的注意力更集中?
(3)一道数学难题,需要讲解24分钟,并且要求学生的注意力至少达到180,那么经过适当安排,老师能否在学生达到所需的状态下讲授完这道题目?
已知函数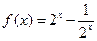 ,
,
(1)若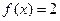 ,求
,求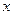 的值;
的值;
(2)若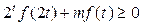 对于
对于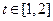 恒成立,求实数
恒成立,求实数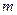 的取值范围。
的取值范围。
若实数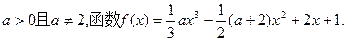
(1)若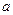 >2,求函数
>2,求函数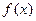 的单调区间;
的单调区间;
(2)若在区间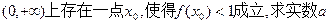 的取值范围.
的取值范围.
(请考生在下面甲、乙两题中任选一题做答,如果多做,则按所做的甲题计分)
甲题:
⑴若关于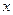 的不等式
的不等式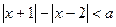 的解集不是空集,求实数
的解集不是空集,求实数 的取值范围;
的取值范围;
⑵已知实数 ,满足
,满足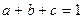 ,求
,求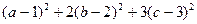 最小值.
最小值.
乙题:
已知曲线C的极坐标方程是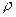 =4cos
=4cos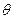 。以极点为平面直角坐标系的原点,极轴为
。以极点为平面直角坐标系的原点,极轴为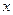 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线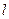 的参数方程是
的参数方程是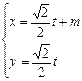 (
(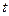 是参数)。
是参数)。
⑴将曲线C的极坐标方程化成直角坐标方程并把直线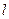 的参数方程转化为普通方程;
的参数方程转化为普通方程;
⑵若过定点 的直线
的直线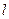 与曲线C相交于A、B两点,且
与曲线C相交于A、B两点,且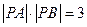 ,试求实数
,试求实数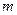 的值。
的值。