计算:
.
设
,
是纯虚数,其中
是虚数单位,则
.
若
,则
.
已知
的内角
所对应边分别为
,若
,则角C的大小是(结果用反三角函数值表示).
设常数
,若
的二项展开式中
项的系数为
,则
方程
的实数解为
在极坐标系中,曲线
与
的公共点到极点的距离为.
盒子中装有编号为1,2,3,4,5,6,7,8,9的九个球,从中任意取出两个,则这两个球的编号之积为偶数的概率是(结果用最简分数表示)
设
是椭圆
的长轴,点
在
上,且
,若
,
,则
的两个焦点之间的距离为
设非零常数
是等差数列
的公差,随机变量
等可能地取值
,则方差
.
若
,则
.
设
为实常数,
是定义在
上的奇函数,当
时,
,若
对一切
成立,则
的取值范围为.
在
平面上,将两个半圆弧
和
、两条直线
和
围成的封闭图形记为
,如图中阴影部分.记
绕
轴旋转一周而成的几何体为Ω,过
作Ω的水平截面,所得截面面积为
,试利用祖暅原理、一个平放的圆柱和一个长方体,得出Ω的体积值为.
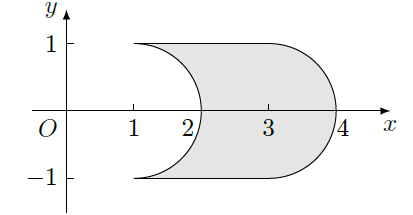
对区间
上有定义的函数
,记
,已知定义域为
的函数
有反函数
,且
,若方程
有解
,则
设常数
,集合
,若
,则
的取值范围为()
| A. |
|
B. |
|
C. |
|
D. |
|
钱大姐常说"便宜没好货",她这句话的意思是:"不便宜"是"好货"的()
| A. |
充分条件 |
B. |
必要条件 |
C. |
充分必要条件 |
D. |
既非充分也非必要条件 |
在数列
中,
,若一个
行
列的矩阵的第
行第
列的元素
,(
)则该矩阵元素能取到的不同数值的个数为()
在边长为1的正六边形
中,记以
为起点,其余顶点为终点的向量分别为
;以
为起点,其余顶点为终点的向量分别为
.若
分别为
的最小值、最大值,其中
,则
满足()
| A. |
|
B. |
|
C. |
|
D. |
|
如图,在长方体
中,
,
,
,证明直线
平行于平面
,并求直线
到平面
的距离.
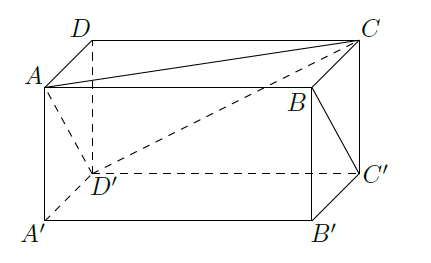
甲厂以
千克/小时的速度运输生产某种产品(生产条件要求
),每小时可获得利润是
元.
(1)要使生产该产品2小时获得的利润不低于3000元,求
的取值范围;
(2)要使生产900千克该产品获得的利润最大,问:甲厂应该选取何种生产速度?并求最大利润.
已知函数
,其中常数
;
(1)若
在
上单调递增,求
的取值范围;
(2)令
,将函数
的图像向左平移
个单位,再向上平移1个单位,得到函数
的图像,区间
(
且
)满足:
在
上至少含有30个零点,在所有满足上述条件的
中,求
的最小值.
如图,已知曲线
,曲线
,
是平面上一点,若存在过点
的直线与
都有公共点,则称
为"
型点".
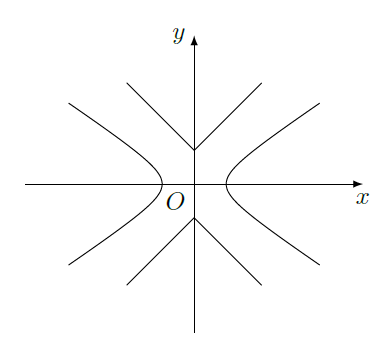
(1)在正确证明
的左焦点是"
型点"时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
(2)设直线
与
有公共点,求证
,进而证明原点不是"
型点";
(3)求证:圆
内的点都不是"
型点".
给定常数
,定义函数
,数列
满足
.
(1)若
,求
及
;
(2)求证:对任意
;
(3)是否存在
,使得
成等差数列?若存在,求出所有这样的
,若不存在,说明理由.


