在△ABC中,角A、B、C的对边分别为a、b、c,满足(c-2a)cosB+bcosC=0
(1)求角B的大小;


(2)若a=2,cosA= ,求c的值
,求c的值
已知半径为120mm的圆上,一条弧的长是144mm,则此弧所对的圆心角的弧度数为
| A.1.2 | B.1.44 | C.1 | D. |
设a<0,角θ的终边经过点P(-3a,4a),那么sinθ+2cosθ=
A. |
B. |
C.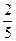 |
D. |
已知向量a=(2,3),b=(-1,2),若a+mb与c=(4,-1)平行,则实数m等于
| A.2 | B.-2 | C. |
D. |
△ABC中,“A=B”是“sinA=sinB”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分又不必要条件 |
函数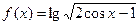 的定义域为
的定义域为
A. (k∈Z) (k∈Z) |
B. (k∈Z) (k∈Z) |
C.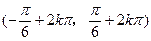 (k∈Z) (k∈Z) |
D. (k∈Z) (k∈Z) |
已知 为第四象限角,则
为第四象限角,则 =
=


A. |
B. |
C. 或 或 |
D.0 |
若对任意x∈R,cos(x+α)+cos(x+β)+cos(x+γ)=0,其中α,β,γ满足0<α<β<γ<2π,则γ-α=
A.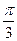 |
B. |
C.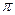 *o*m *o*m |
D. |
已知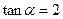 ,则
,则 =____________.
=____________.


在△ABC中,已知sinA=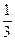 ,则A=____________.(用反三角函数表示)w
,则A=____________.(用反三角函数表示)w
设点A(2,0),B(4,2),点P在直线AB上,且| |=2|
|=2|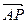 |,则点P的坐标为____________.
|,则点P的坐标为____________.
已知函数 ,给出下列命题:
,给出下列命题:

 w
w
① 的图象可以看作是由y=sin2x的图象向左平移
的图象可以看作是由y=sin2x的图象向左平移 个单位而得;
个单位而得;
② 的图象可以看作是由y=sin(x+
的图象可以看作是由y=sin(x+ )的图象保持纵坐标不变,横坐标缩小为原来的
)的图象保持纵坐标不变,横坐标缩小为原来的 而得;
而得;
③函数y=| |的最小正周期为
|的最小正周期为 ;
;
④ 函数y=| |是偶函数.
|是偶函数.
其中正确的结论是: .(写出你认为正确的所有结论的序号)
在△ABC中,已知tanA=3,sinB= ,求角C的大小.
,求角C的大小.
若cosθ>0,sin2θ<0,则角θ是


| A.第一象限角 | B.第二象限角 |
| C.第三象限角 | D.第四象限角 |
 的值是
的值是
| A. |
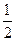
|
B. |

|
C. |

|
D. |

|
如图,在平行四边形ABCD中,AD=2AB=2,∠BAD=60º,M、N分别是对角线BD、AC上的点,AC、BD相交于点O,已知BM= BO,ON=
BO,ON= OC.设向量
OC.设向量 =a,
=a, =b
=b


(1)试用a,b表示 ;w
;w
(2)求| |.
|.

已知向量a=(sinx, cosx),b=(2sinx,sinx),设
cosx),b=(2sinx,sinx),设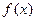 =a·b-1
=a·b-1
(1)求函数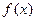 ,并求使函数取得最小值的x的集合
,并求使函数取得最小值的x的集合
(2)若方程 在x∈[
在x∈[ ,
, ]上有实数解,求实数
]上有实数解,求实数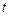 的取值范围.
的取值范围.
已知△ABC是边长为1的正三角形,则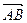 在
在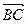 方向上的投影为
方向上的投影为


A. |
B. |
C. |
D. |
海上两个小岛A,B到海洋观察站C的距离都是a km,小岛A在观察站C北偏东 ,小岛B在观察站C南偏东
,小岛B在观察站C南偏东 ,则A与B的距离是
,则A与B的距离是
| A.akm | B. akm akm |
C.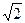 akm akm |
D.2akm |
下列式子中正确的是

 w
w
A.sin1<  º º |
B.sin1<cos1 |
C.sin1= |
D.sin1<tan1 |