设集合 ,
, ,则A∩B是
,则A∩B是
A. |
B. |
C. |
D. |
若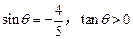 ,则
,则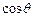 =
=
A.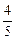 |
B.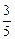 |
C.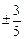 |
D. |
已知函数 ,
, ,则
,则 是
是
A.最小正周期为 的偶函数 的偶函数 |
B.最小正周期为 的偶函数 的偶函数 |
C.最小正周期为 的奇函数 的奇函数 |
D.最小正周期为 的奇函数 的奇函数 |

条件语句的一般形式如右图所示,其中F表示的是
| A.条件 |
| B.条件语句 |
| C.满足条件时执行的内容 |
| D.不满足条件时执行的内容 |
 的值为
的值为
A. |
B. |
C. |
D. |
.如图,在一个边长为 cm的正方形内部画一个边长为
cm的正方形内部画一个边长为 cm的小正方形,向大正方形内随机投点,则所投的点落入小正方形内的概率是
cm的小正方形,向大正方形内随机投点,则所投的点落入小正方形内的概率是
A. B.
C. D.
若ABCD为正方形,E是CD的中点,且 =,
=, =,则
=,则 等于
等于
A.+ |
B.- |
C.+ |
D.- |
已知向量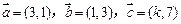 ,若
,若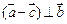 ,则实数
,则实数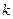 等于
等于
A.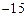 |
B.15 |
| C.21 | D.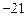 |
从一批产品中取出三件,设A表示:“三件产品全不是次品”,B表示:“三件产品全是次品”,C表示:“三件产品不全是次品”,则下列结论正确的是
| A.A与C互斥 |
| B.B与C互斥 |
| C.任两个均互斥 |
| D.任两个均不互斥 |

在如图给出的算法流程图中,输出的结果等于
| A.21 |
| B.22 |
| C.23 |
| D.42 |
一个容量为100的样本,其数据的分组与各组的频数如下表:
| 组别 |
(0,10] |
(10,20] |
(20,30] |
(30,40] |
(40,50] |
(50,60] |
(60,70] |
| 频数 |
12 |
13 |
24 |
15 |
16 |
13 |
7 |
则样本数据落在(10,40]上的频率为
| A.0.13 | B.0.39 |
| C.0.52 | D.0.64 |
将函数 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象向左平移
的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象向左平移 个单位,得到的图象对应的解析式是
个单位,得到的图象对应的解析式是
A. |
B. |
C. |
D. |
一个田径队有男运动员20人,女运动员10人,比赛后立刻用分层抽样的方法,从全体队员中抽出一个容量为6人的样本进行兴奋剂检查,则其中男运动员应抽 人.
施化肥量x kg与水稻产量y kg在一定范围内线性相关,若回归直线方程为=5x+250,当施化肥量为80 kg时,预计水稻的产量为_________.
规定运算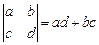 ,若
,若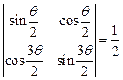 ,则
,则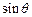 = .
= .
已知a、b是直线, 、
、 、
、 是平面,给出下列命题:
是平面,给出下列命题:
①若 ∥
∥ ,a
,a
 ,则a∥
,则a∥ ;
;
②若a、b与 所成角相等,则a∥b;
所成角相等,则a∥b;
③若 ⊥
⊥ 、
、 ⊥
⊥ ,则
,则 ∥
∥ ;
;
④若a⊥ ,a⊥
,a⊥ ,则
,则 ∥
∥ .
.
其中正确的命题的序号是_________.
(本小题满分10分)
求经过直线 与
与 的交点和坐标原点的直线
的交点和坐标原点的直线 的方程.
的方程.
(本小题满分12分)
已知向量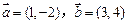 .
.
(1)求向量 的坐标;
的坐标;
(2)当实数 为何值时,
为何值时,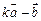 与
与 共线.
共线.
(本小题满分12分)
已知函数 满足
满足 .
.
(1)求常数c的值;
(2)若 ,求实数x的值.
,求实数x的值.
(本小题满分12分)
同时掷两颗骰子,计算:
(1)向上的点数相同的概率;
(2)向上的点数之和是5的概率.
(本小题满分12分)
甲、乙两位学生参加数学竞赛培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲 82 81 79 78 95 88 93 84
乙 92 95 80 75 83 80 90 85
(1)用茎叶图表示这两组数据;若将频率视为概率,对甲学生在培训后参加的一次数学竞赛成绩进行预测,求甲的成绩高于80分的概率;
(2)现要从中选派一人参加数学竞赛,从统计学的角度(在平均数、方差或标准差中选两个)考虑,你认为选派哪位学生参加合适?请说明理由.
标准差公式: .
.
(本小题满分12分)
已知函数 .
.
(1)求实数 的值;
的值;
(2)当xÎ 时,求函数
时,求函数 的值域.
的值域.