某地区有300家商店,其中大型商店有30家,中型商店有75家,小型商店有195家. 为了掌握各商店的营业情况,要从中抽取一个容量为20的样本. 若采用分层抽样的方法,抽取的中型商店数是( )
| A.2 | B.5 | C.3 | D.13 |
cos(- )的值是( )
)的值是( )
A.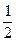 B.-
B.-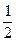 C.
C.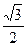 D.-
D.-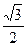
若 ,则向量
,则向量 的坐标是( )
的坐标是( )
| A.(3,-4) | B.(-3,4) | C.(3,4) | D.(-3,-4) |
口袋内装有一些大小相同的红球、白球和黑球,从中摸出1个球,如果摸出红球的概率是0.42,摸出白球的概率是0.28,那么摸出黑球的概率是( )
| A.0.42 | B.0.28 | C.0.3 | D.0.7 |
十进制数25转化为二进制数为( )
A.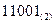 |
B.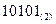 |
C. |
D.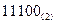 |
化简 的结果为( )
的结果为( )
| A.1 | B.-1 | C.tanα | D.-tanα |
已知x与y之间的一组数据:
| x |
0 |
1 |
2 |
3 |
| y |
1 |
3 |
5 |
7 |
则y与x的线性回归方程为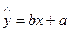 必过点( )
必过点( )
A.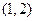 |
B.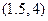 |
C.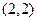 |
D. |
如右图程序输出的m是( )
| A.5 | B.6 | C.24 | D.120 |
|
要得到函数 的图像,只要把函数y="3sin2x" 图像
的图像,只要把函数y="3sin2x" 图像
A.向右平移 个单位 个单位 |
B.向左平移 个单位 个单位 |
C.向右平移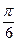 个单位 个单位 |
D.向左平移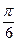 个单位 个单位 |
函数 是 ( )
是 ( )
A.最小正周期为 的偶函数 的偶函数 |
B.最小正周期为 的奇函数 的奇函数 |
C.最小正周期为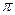 的偶函数 的偶函数 |
D.最小正周期为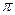 的奇函数 的奇函数 |
如图,函数 的图象经过点
的图象经过点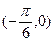 、
、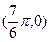 ,且该函数的最大值为2,最小值为-2,则该函数的解析式为 ( )
,且该函数的最大值为2,最小值为-2,则该函数的解析式为 ( )
A.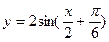 |
B. |
C.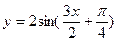 |
D. |
已知 为正实数,函数
为正实数,函数 在
在 上为增函数,则 ( )
上为增函数,则 ( )
A. ≤ ≤ |
B. ≤2 ≤2 |
C. ≤ ≤ |
D. ≥2 ≥2 |
如图,某人向圆内投镖,如果他每次都投入圆内,
那么他投中正方形区域的概率为
若向量 ,
, 满足
满足 ,
, 与
与 的夹角为600,那么
的夹角为600,那么 =数与平均数相等,则这组数据中位数是
=数与平均数相等,则这组数据中位数是
已知某班4个小组的人数分别为10、10、x、8,这组数据的中位数是____
对于函数 ,给出下列命题
,给出下列命题
①图像关于原点成中心对称; ②图像关于直线 对称;
对称;
③函数 的最大值是3; ④函数的周期是
的最大值是3; ④函数的周期是 ;
;
⑤函数的一个单调增区间是 ;其中正确命题的序号为
;其中正确命题的序号为
(本小题满分10分)
若 ,
, ,且
,且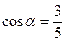 ,
,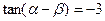 ,求下列各值.
,求下列各值.
(1)  (2)
(2) 
(本小题满分 12分)
12分)
根据下面的要求,求满足 的最小的自然数n。
的最小的自然数n。
(1)画出执行该问题的程序框图;
(2)下图是解决该问题的一个程序,但有2处错误,请找出错误并予以更正。
已知 ,若
,若 ,
,
 ,
,
(1)求 ;
;
(2)求 的夹角。
的夹角。
上海某学校要从艺术节活动中所产生的4名书法比赛一等奖的同学和2名绘画比赛一等奖的同学中选出2名志愿者,参加即将在上海举行的世博会的志愿服务工作.
(1)求选出的两名志愿者都是获得书法比赛一等奖的同学的概率;
(2)求选出的两名志愿者中一名是获得书法比赛一等奖,另一名是获得绘画比赛一等奖的同学的概率.
已知函数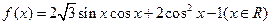
(1)求函数 的最小正周期及在区间
的最小正周期及在区间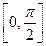 上的最大值和最小值;
上的最大值和最小值;
(2)若 ,求
,求 的值。
的值。