某班有学生54人,有4张上海世博会门票,现根据学生的学号,用系统抽样的方法分给4位学生.若已知3号,29号,42号学生已被抽中,那么还有一个被抽到的学生学号是 ▲
如图是某校主持人大赛上七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数为 ▲ 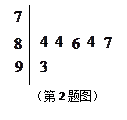
命题“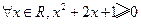 ”的否定是 ▲
”的否定是 ▲
连续两次抛掷一枚质地均匀的硬币,则仅有一次正面朝上的概率为 ▲
阅读如图所示的程序框图,若输入的 是
是 ,则输出的变量
,则输出的变量 的值是 ▲
的值是 ▲ 
函数 的定义域是 ▲
的定义域是 ▲
已知函数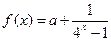 ,若
,若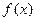 为奇函数,则
为奇函数,则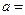 ▲
▲
幂函数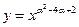 (
(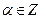 )的图象在第二象限内为增函数,则
)的图象在第二象限内为增函数,则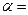 ▲
▲
在0到1之间任取两个实数,则它们的平方和大于1的概率是 ▲
已知 是周期为
是周期为 的奇函数,当
的奇函数,当 时,
时,
若 ,则将
,则将 从小到大排列为 ▲
从小到大排列为 ▲
观察下列等式:
由此猜测第 个等式为 ▲
个等式为 ▲
方程 根的个数为 ▲
根的个数为 ▲
已知 在
在 上是
上是 的减函数,则实数
的减函数,则实数 取值范围为 ▲
取值范围为 ▲
已知函数
 和函数
和函数 ,若对于任意
,若对于任意 ,总存在
,总存在 ,使得
,使得 成立,则实数
成立,则实数 的取值范围为 ▲
的取值范围为 ▲
某校从参加高一年级期末考试的学生中抽出60名学生,并统计了他们的物理成绩(成绩均为整数且满分为100分),把其中不低于50分的分成五段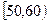 ,
,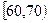 …
…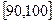 后画出如下部分频率分布直方图.观察图形的信息,回答下列问题
后画出如下部分频率分布直方图.观察图形的信息,回答下列问题
(1)求出物理成绩低于50分的学生人数
(2)估计这次考试物理学科及格率(60分及以上为及格)
(3)从物理成绩不及格的学生中选1人,求他们成绩至少有一个低于50分的概率
 |
已知全集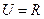 ,集合
,集合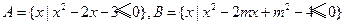 ,
,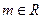 .
.
(1)若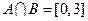 ,求实数
,求实数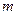 的值;
的值;
(2)若“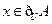 ”是“
”是“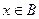 ”的必要不充分条件,求实数
”的必要不充分条件,求实数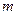 的取值范围.
的取值范围.
已知 为
为 上的奇函数,当
上的奇函数,当 时,
时, 为二次函数,且满足
为二次函数,且满足 ,不等式组
,不等式组 的解集是
的解集是 .
.
(1)求函数 的解析式
的解析式
(2)作出 的图象并根据图象讨论关于
的图象并根据图象讨论关于 的方程:
的方程:
 根的个数
根的个数
已知 ,
, 
(1)当 时
时
1解关于 的不等式
的不等式
2当 时,不等式
时,不等式 恒成立,求
恒成立,求 的取值范围
的取值范围
(2)证明不等式
2010年上海世博会某国要建一座八边形(不一定为正八边形)的展馆区(如图),它的主体造型的平面图是由二个相同的矩形 和
和 构成的面积为
构成的面积为 m2的十字型地域,计划在正方形
m2的十字型地域,计划在正方形 上建一座“观景花坛”,造价为
上建一座“观景花坛”,造价为 元/m2,在四个矩形上(图中阴影部分)铺花岗岩地坪,造价为
元/m2,在四个矩形上(图中阴影部分)铺花岗岩地坪,造价为 元/m2,再在四个空角(如
元/m2,再在四个空角(如 等)上铺草坪,造价为
等)上铺草坪,造价为 元/m2. 设总造价为
元/m2. 设总造价为 元,
元, 长为
长为 m.
m. (1)用
(1)用 表示矩形
表示矩形 的边
的边 的长
的长
(1)试建立 与
与 的函数关系
的函数关系
(2)当 为何值时,
为何值时, 最小?并求这个最小值
最小?并求这个最小值
在区间 上,如果函数
上,如果函数 为增函数,而函数
为增函数,而函数 为减函数,则称函数
为减函数,则称函数 为“弱增”函数.已知函数
为“弱增”函数.已知函数
(1)判断函数 在区间
在区间 上是否为“弱增”函数
上是否为“弱增”函数
(2)设 ,证明
,证明
(3)当 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围