若直线经过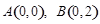
两点，则直线AB的倾斜角为
| A．30° | B．45° | C．90° | D．0° |
直线在平面外是指
| A．直线与平面没有公共点 | B．直线与平面相交 |
| C．直线与平面平行 | D．直线与平面最多只有一个公共点 |
已知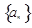
是等比数列，
，则公比
等于
| A．2 | B． |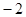
C． |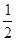
D． |
圆
的圆心坐标和半径分别为
A． |
B． |
C． |
D． |
在
中,
分别为内角
的对边，且
则
等于
| A．30° | B．45° | C．60° | D．120° |
满足线性约束条件
的目标函数
的最大值是
A． |
B． |
C． |
D． |
数列
的通项公式是
其前
项和为
则项数等于
| A．6 | B．9 | C．10 | D．13 |
直线
恒过定点
，且点在直线
（
）上，则
的最小值为
A． |
B． |
C． |
D． |
直线
与坐标轴围成的三角形的面积为 .
在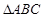
中
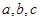分别为内角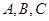
的对边,已知
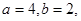则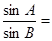
______.
关于
的不等式
的解集为
则实数
.
过点
的直线
被圆
所截得的弦长为10，则直线的方程为 .
函数
的定义域为实数集
，实数
的取值范围为 .
已知数列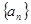
：
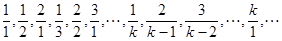, 则(1)
；
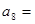(2)在这个数列中，若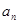
是第８个值等于1的项，则
.
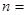等差数列
的前
项和为
，已知
.
（1）求通项公式
；
（2）若
求.
已知两条直线
,
相交于
点.
（1）求交点的坐标；
（2）求过点且与直线
垂直的直线
的方程.
如图，当甲船位于A处时获悉，在其正东方向相距20海里的B处有一艘渔船遇险等待营救，甲船立即前往救援，同时把消息告之在甲船的南偏西30°,相距10海里C处的乙船.
（1）求处于C处的乙船和遇险渔船间的距离；
（2）设乙船沿直线CB方向前往B处救援，求∠ACB的正弦值.
已知
是正方形，
⊥面,且
，
是侧棱
的中点.
（1）求证
∥平面
；
（2）求证平面
平面
；
（3）求直线
与底面所成的角的正切值.
已知圆
和点
（1）若过点
有且只有一条直线与圆
相切，求正实数
的值，并求出切线方程；（2）若
，过点的圆的两条弦
互相垂直，设
分别为圆心到弦的距离．
（Ⅰ）求
的值；
（Ⅱ）求两弦长之积
的最大值．
已知数列
满足：
且
.（1)求数列的前三项；（2）是否存在一个实数
，使数列
为等差数列？若存在，求出的值；若不存在，说明理由；（3）求数列的前
项和
.