设函数
，当自变量
由
改变到
时，函数值的改变量
等于
A． |
B． |
C． |
D． |
下列结论中正确的是( )
| A．导数为零的点一定是极值点 |
B．如果在 附近的左侧 ，右侧 ，那么 是极大值 |
| C．如果在附近的左侧，右侧，那么是极小值 |
| D．如果在附近的左侧，右侧，那么是极大值 |
在下列函数中，最小值为2的是
A． |
B． |
C． |
D． |
下表是降耗技术改造后生产甲产品过程中记录的产量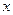
（吨）与相应的 生产能耗
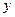（吨标准煤）的几组对应数据，根据表中提供的数据，求出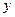关于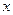的线性回归方程
+
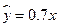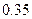，那么表中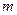
的值为 ( ).
|
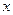3 |
4 |
5 |
6 |
||||
|
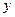2.5 |
|
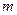4 |
4．5
|
用数学归纳法证明“当n 为正奇数时，
能被
整除”，在第二步时，正确的证法是（ ）
A．假设 ，证明 命题成立 |
B．假设 ，证明命题成立 |
C．假设 ，证明命题成立 |
D．假设，证明 命题成立 |
复数z对应的点在第二象限，它的模为3，实部是
，则
是 （ ）
| A．+2i |
B．-2i |
C． +2i |
D．-2i |
（ ）
A． |
B． |
C． |
D． |
（
）展开式中
的系数为10，则实数a等于 （ ）
| A．２ | B． |
C． 1 | D．－１ |
从0，1，2，…，9这10个数字中，任取两个不同数字作为平面直角坐标系中点的坐标，能够确定不在x轴上的点的个数是（ ）
| A．100 | B．90 | C．81 | D．72 |
经过点M(1，5)且倾斜角为
的直线，以定点M到动 点P的位移t为参数的参数方程是 ( )
A． |
B． |
C． |
D． |
在
中，若
，则
的外接圆半径
，将此结论拓展到空间，可得出的正确结论是：在四面体
中，若
两两垂直，
，则四面体
的外接球半径
；
设随机变量ξ的概率分布列为
，
，则
．
.
14. 不等式
的解集为
从如图所示的长方形区域内任取一个点M（x,y）, 则点M 取自阴影部分的概率为 .
（本小题满分12分）. 一物体沿直线以速度
（
的单位为:秒,
的单位为:米/秒）的速度作变速直线运动，求该物体从时刻t=0秒至时刻 t=5秒间运动的路程?
（本小题满分12分）用数学归纳法证明：
（本小题满分12分）圆
和圆
的极坐标方程分别为
．
（1）把圆和圆的极坐标方程化为直角坐标方程；
（2）求经过圆，圆两个交点的直线的直角坐标方程．
（本小题满分12分） 函数
，
（1）若
，解不等式
； （2）如果
，
，求a的取值范围
（本小题满分13分）已知函数
（１）求函数
在
上的最大值和最小值．
（２）求证：在区间［１，+
，函数的图象，在函数
的图象下方。
（本小题满分14分）
现在要对某个学校今年将要毕业的900名高三毕业生进行乙型肝炎病毒检验，可以利用两种方法．①对每个人的血样分别化验，这时共需要化验900次；②把每个人的血样分成两份，取其中m个人的血样各一份混合在一起作为一组进行化验，如果结果为阴性，那么对这m个人只需这一次检验就够了；如果结果为阳性，那么再对这m个人的另一份血样逐个化验，这时对这m个人一共需要m+1次检验．据统计报道，对所有人来说，化验结果为阳性的概率为0.1．
（1）求当m=3时，一个小组经过一次检验就能确定化验结果的概率是多少？
（2）试比较在第二种方法中，m=4和m=6哪种分组方法所需要的化验次数更少一些？