在复平面内,复数 所对应的点位于( )
所对应的点位于( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
下列表述正确的是( )
①归纳推理是由部分到整体的推理;②归纳推理是由一般到一般的推理;
③演绎推理是由一般到特殊的推理;④类比推理是由特殊到一般的推理;
⑤类比推理是由特殊到特殊的推理。
| A.①②③; | B.②③④; | C.②④⑤; | D.①③⑤。 |
在下列函数中,最小值为2的是
A. |
B. |
C. |
D. |
下表是降耗技术改造后生产甲产品过程中记录的产量 (吨)与相应的 生产能耗
(吨)与相应的 生产能耗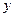 (吨标准煤)的几组对应数据,根据表中提供的数据,求出
(吨标准煤)的几组对应数据,根据表中提供的数据,求出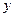 关于
关于 的线性回归方程
的线性回归方程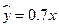 +
+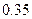 ,那么表中
,那么表中 的值为
的值为
 |
3 |
4 |
5 |
6 |
||||
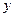 |
2.5 |
 |
4 |
4.5
|
根据右边程序框图,当输入10时,输出的是( )
| A.12 | B.19 | C.14.1 | D.-30 |
复数z对应的点在第二象限,它的模为3,实部是 ,则
,则 是 ( )
是 ( )
A. +2i +2i |
B. -2i -2i |
C. +2i +2i |
D. -2i -2i |
 ( )
( )
A. |
B. |
C. |
D. |
参数方程为 表示的曲线是( )
表示的曲线是( )
| A.一条直线 | B.两条直线 | C.一条射线 | D.两条射线 |
从0,1,2,…,9这10个数字中,任取两个不同数字作为平面直角坐标系中点的坐标,能够确定不在x轴上的点的个数是( )
| A.100 | B.90 | C.81 | D.72 |
经过点M(1,5)且倾斜角为 的直线,以定点M到动 点P的位移t为参数的参数方程是 ( )
的直线,以定点M到动 点P的位移t为参数的参数方程是 ( )
A. |
B. |
C. |
D. |
在 中,若
中,若 ,则
,则 的外接圆半径
的外接圆半径 ,将此结论拓展到空间,可得出的正确结论是:在四面体
,将此结论拓展到空间,可得出的正确结论是:在四面体 中,若
中,若 两两垂直,
两两垂直, ,则四面体
,则四面体 的外接球半径
的外接球半径 ;
;
 =__________;
=__________;
 左焦点的坐标是_________________
左焦点的坐标是_________________
不等式 的解集为
的解集为
 .
.
(本小题满分12分). 实数m取什么数值时,复数 分别是: (1)实数? (2)虚数? (3)纯虚数?
分别是: (1)实数? (2)虚数? (3)纯虚数?
(本小题满分12分)
已知 ,判断
,判断 与
与 的大小,并证明你的结论.
的大小,并证明你的结论.
(本小题满分12分)圆 和圆
和圆 的极坐标方程分别为
的极坐标方程分别为 .
.
(1)把圆 和圆
和圆 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)求经过圆 ,圆
,圆 两个交点的直线的直角坐标方程.
两个交点的直线的直角坐标方程.
(本小题满分12分)已知点 是圆
是圆 上的动点,
上的动点,
(1)求 的取值范围;
的取值范围;
(2)若 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
(本小题满分13分)函数 ,
,
(1)若 ,解不等式
,解不等式 ; (2)如果
; (2)如果 ,
, ,求a的取值范围
,求a的取值范围
(本小题满分14分)
已知数列 的前n项和为
的前n项和为 ,且
,且 ,
,
(1)试计算 ,并猜想
,并猜想 的表达式;
的表达式;
(2) 证明你的猜想,并求出 的表达式。
的表达式。