从“ ”、“
”、“ ”、“
”、“ ”中选择适当的符号填空:
”中选择适当的符号填空:
① ▲
▲  ;②
;② A∪B ▲
A∪B ▲  A∩B.
A∩B.
若命题p的逆命题是q,命题p的逆否命题是r,则q与r的命题关系是 ▲ .
 是虚数单位.已知
是虚数单位.已知 ,则复数z对应的点落在第 ▲ 象限.
,则复数z对应的点落在第 ▲ 象限.
已知命题P: R,
R,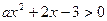 .如果命题
.如果命题 P是真命题,那么
P是真命题,那么 的范围是 ▲ .
的范围是 ▲ .
已知双曲线的两条渐近线方程为 ,则双曲线方程为 ▲ .
,则双曲线方程为 ▲ .
已知在复平面内,定点M与复数m=1+2i对应,动点Z与复数 (
( R)对应,那么不等式
R)对应,那么不等式 ≤2的点Z的集合表示的图形面积为 ▲ .
≤2的点Z的集合表示的图形面积为 ▲ .
已知圆x2+y2-6x-7=0与抛物线y2=-2px (p>0)的准线相切,则p= ▲ .
设中心在原点的椭圆离心率为e,左、右两焦点分别为F1、F2,抛物线 以F2为焦点,点P为抛物线和椭圆的一个交点,若PF2与x轴成45°,则e的值为 ▲ .
以F2为焦点,点P为抛物线和椭圆的一个交点,若PF2与x轴成45°,则e的值为 ▲ .
已知函数 ,则
,则 取得极值时的x值为 ▲ .
取得极值时的x值为 ▲ .
已知函数 ,若
,若 ,则函数的值域为 ▲ .
,则函数的值域为 ▲ .
已知函数 的图象如图,
的图象如图,
则函数 的草图为 ▲ .
的草图为 ▲ .
已知三次方程 有三个实数根,它们分别可作为抛物线、双曲线、椭圆的离心率,则实数a的取值范围是 ▲ .
有三个实数根,它们分别可作为抛物线、双曲线、椭圆的离心率,则实数a的取值范围是 ▲ .
请阅读下列材料:若两个正实数 满足
满足 ,那么
,那么 .证明:构造函数
.证明:构造函数 ,因为对一切实数
,因为对一切实数 ,恒有
,恒有 ,所以
,所以 ,从而得
,从而得 ,所以
,所以 .根据上述证明方法,若
.根据上述证明方法,若 个正实数满足
个正实数满足 时,你能得到的结论为 .(不必证明)
时,你能得到的结论为 .(不必证明)
如图,坐标纸上的每个单元格的边长为1,
由下往上的六个点:1,2,3,4,5,6的横纵坐标
分别对应数列 (n∈Z*)的前12项,
(n∈Z*)的前12项,
如下表所示:
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
按如此规律下去,则 = ▲ .
= ▲ .
已知复数 ,
, (
( R).
R).
(1)在复平面中,若 (O为坐标原点,复数
(O为坐标原点,复数 ,
, 分别对应点
分别对应点 ),求
),求 满足的关系式;
满足的关系式;
(2)若 ,
, ,求
,求 ;
;
设命题p:函数 的定义域为R;
的定义域为R;
命题q:关于x的不等式 ,对一切正实数均成立.
,对一切正实数均成立.
(1)如果p是真命题,求实数a的取值范围;
(2)如果命题“p或q”为真命题且“p且q”假命题,求实数a的取值范围.
已知直线 :
: 过抛物线
过抛物线 的焦点.
的焦点.
(1)求抛物线方程;
(2)设抛物线的一条切线 ,若
,若 ∥
∥ ,求切点坐标.
,求切点坐标.
(方法不唯一)
已知
 R,且
R,且 ,是否存在虚数
,是否存在虚数 同时满足:
同时满足:
① ;②
;② .
.
若存在,请求出复数z;若不存在,请说明理由.
某地建一座桥,两端的桥墩已建好,这两桥墩相距m米,余下的工程只需要建两端桥墩之间的桥面和桥墩.经预测,一个桥墩的工程费用为256万元,距离为x米的相邻两墩之间的桥面工程费用为 万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为y万元.
万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为y万元.
(1)试写出y关于x的函数关系式;
(2)当m=640米时,需新建多少个桥墩才能使y最小?
【求导参考公式: ;
; ;
; ;
; 】
】
已知双曲线 左右两焦点为
左右两焦点为 ,P为右支上一点,
,P为右支上一点, ,
, 于H,
于H, ,
, .
.
(1)求双曲线的离心率e的取值范围;
(2)当e取得最大值时,过 ,P的圆截y轴的线段长为4,求该圆方程.
,P的圆截y轴的线段长为4,求该圆方程.