不等式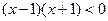 的解集为 ▲ .
的解集为 ▲ .
函数 最小值是 ▲ .
最小值是 ▲ .
已知数列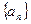 的前n项和
的前n项和
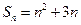 ,则
,则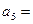 ▲ .
▲ .
在 中,
中, ,则最大角的余弦值是 ▲ .
,则最大角的余弦值是 ▲ .
已知 则
则 与
与 的大小关系为 ▲ .
的大小关系为 ▲ .
执行下面的程序框图,输出的 ▲ .
▲ .
下图是一次考试结果的频率分布直方图,若规定60分以上(含60)为考试合格,则这次考试的合格率为 ▲ .
(第6题图)
在 中,若
中,若 , 则
, 则 的面积是 ▲
的面积是 ▲  .
.
已知实数 满足约束条件
满足约束条件 则
则 的最大值为 ▲ .
的最大值为 ▲ .
点 为周长等于3的圆周上的一个定点,若在该圆周上随机取一点
为周长等于3的圆周上的一个定点,若在该圆周上随机取一点 ,则劣弧
,则劣弧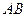 的长度小于1的概率为 ▲ .
的长度小于1的概率为 ▲ .
已知函数 ,
, 仿照等差数列求和公式的推导方法,化简:
仿照等差数列求和公式的推导方法,化简: ▲ .
▲ .
若不等式 ≥
≥ 对任意的正数
对任意的正数 总成立,则正数
总成立,则正数 的取值范围为 ▲ .
的取值范围为 ▲ .
在实数集R上定义运算 ,若不等式
,若不等式 对任意实数
对任意实数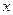 都成立,则实数
都成立,则实数 的取值范围是 ▲ .
的取值范围是 ▲ .
已知点 在两直线
在两直线 和
和 之间
之间 的带状区域内(含边界)运动,则
的带状区域内(含边界)运动,则 的最小值为 ▲ .
的最小值为 ▲ .

随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如下图 .
⑴根据茎叶图判断哪个班的平均身高较高;
⑵计算甲班的样本方差.
⑴在 中,已知
中,已知 求此三角形最小边的长;
求此三角形最小边的长; ⑵在
⑵在 中
中 ,已知
,已知 ,求
,求 .
.
从3名男生和2名女生中任选2人参加学校演讲比赛。
⑴求所选 2人恰有
2人恰有 名女生的概率;
名女生的概率;
⑵求所选2人中至少有 名
名 女生的概率.
女生的概率.
某村计划建造一个室内面积为800 的矩形蔬菜温室。在温室内,沿左、右两侧与后侧内墙各保留1
的矩形蔬菜温室。在温室内,沿左、右两侧与后侧内墙各保留1 宽的通道,沿前侧内墙保留3
宽的通道,沿前侧内墙保留3 宽的空地,当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少?
宽的空地,当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少?
已知
⑴当不等式 的解集为
的解集为 时,求实数
时,求实数 的值;
的值;
⑵若对任意实数 ,
, 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
⑶设 为常数,解关于
为常数,解关于 的不等式
的不等式 .
.
设数列 的前
的前 项和为
项和为 ,若对任意
,若对任意 ,都有
,都有 .
.
⑴求数列 的首项;
的首项;
⑵求证:数列 是等比数列,并求数列
是等比数列,并求数列 的通项公式;
的通项公式;
⑶数列 满足
满足 ,问是否存在
,问是否存在 ,使得
,使得 恒成立?如果存在,求出
恒成立?如果存在,求出 的值,如果不存在,说明理由.
的值,如果不存在,说明理由.