函数 的定义域为( )
的定义域为( )
A. |
B. |
C. |
D. |
设 R,
R, 是虚数单位,则“
是虚数单位,则“ ”是“复数
”是“复数 为纯虚数”的( )
为纯虚数”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
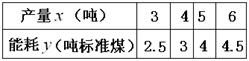
小明同学根据右表记录的产量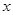 (吨)与能耗
(吨)与能耗 (吨标准煤)对应的四组数据,用最小二乘法求出了
(吨标准煤)对应的四组数据,用最小二乘法求出了 关于
关于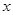 的线性回归方程
的线性回归方程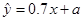 ,据此模型预报产量为7万吨时能耗为( )
,据此模型预报产量为7万吨时能耗为( )
A. |
B.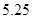 |
C. |
D.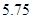 |
设 为等比数列
为等比数列 的前
的前 项和,
项和, ,则
,则 的值为( )
的值为( )
A. |
B. |
C. 11 | D. |
已知 为不同的直线,
为不同的直线, 为不同的平面,给出下列四个命题:
为不同的平面,给出下列四个命题:
①若 ,则
,则 ; ②若
; ②若 ,则
,则 ;
;
③若 ,则
,则 ; ④若
; ④若 ,则
,则 .
.
其中所有正确命题的序号是( )
| A.①② | B.②③ | C.①③ | D.①④ |
曲线 的一条切线平行于直线
的一条切线平行于直线 ,则除切点外切线与曲线的另一交点坐标可以是( )
,则除切点外切线与曲线的另一交点坐标可以是( )
A. |
B. |
C. |
D. |
已知函数 且
且 则
则 的值为( )
的值为( )
A. |
B. |
C. |
D. . . |
已知角 的顶点在坐标原点,始边与
的顶点在坐标原点,始边与 轴的正半轴重合,
轴的正半轴重合, ,角
,角 的终边与单位圆交点的横坐标是
的终边与单位圆交点的横坐标是 ,角
,角 的终边与单位圆交点的纵坐标是
的终边与单位圆交点的纵坐标是 ,则
,则 的值为( )
的值为( )
A. |
B. |
C. |
D. |
过双曲线 的右焦点
的右焦点 作与
作与 轴垂直的直线,分别与双曲线及其渐近线交于点
轴垂直的直线,分别与双曲线及其渐近线交于点 (均在第一象限内),若
(均在第一象限内),若 ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A. |
B. |
C. |
D. |
若向量 的夹角为
的夹角为 ,
, ,则
,则 = .
= .
已知一条直线的参数方程是 ,另一条直线的方程是
,另一条直线的方程是 ,则两直线的交点与点
,则两直线的交点与点 间的距离是 .
间的距离是 .
根据《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20~80  /100
/100 (不含80)之间,属于酒后驾车;血液酒精浓度在80
(不含80)之间,属于酒后驾车;血液酒精浓度在80 /100
/100 (含80)以上时,属醉酒驾车.据《法制晚报》报道,2013年1月1日至1月7日,全国查处酒后驾车和醉酒驾车共38800人,如图是对这38800人酒后驾车血液中酒精含量进行检测所得结果的频率分布直方图,则属于醉酒驾车的人数约为______.
(含80)以上时,属醉酒驾车.据《法制晚报》报道,2013年1月1日至1月7日,全国查处酒后驾车和醉酒驾车共38800人,如图是对这38800人酒后驾车血液中酒精含量进行检测所得结果的频率分布直方图,则属于醉酒驾车的人数约为______.
某程序框图如右图所示,若判断框内 ,且
,且 时,输出的
时,输出的 ,则判断框内
,则判断框内 应为 .
应为 .
如图1,小正方形 的面积为1,把它的各边延长一倍得到新正方形
的面积为1,把它的各边延长一倍得到新正方形 ,再把正方形
,再把正方形 的各边延长一倍得到正方形
的各边延长一倍得到正方形 (如图2),如此进行下去,正方形
(如图2),如此进行下去,正方形 的面积为 .(用含有
的面积为 .(用含有 的式子表示,
的式子表示, 为正整数)
为正整数)
随着经济的发展,人们生活水平的提高,中学生的营养与健康问题越来越得到学校与家长的重视. 从学生体检评价报告单了解到某校3000名学生的体重发育评价情况,得右表:
| |
偏瘦 |
正常 |
肥胖 |
| 女生(人) |
300 |
865 |
 |
| 男生(人) |
 |
885 |
 |
已知从这批学生中随机抽取1名学生,抽到偏瘦男生的概率为0.15.
(Ⅰ)求 的值;
的值;
(Ⅱ)若用分层抽样的方法,从这批学生中随机抽取60名,问应在肥胖学生中抽出多少名?
(Ⅲ)已知 ,
, ,求肥胖学生中男生不少于女生的概率.
,求肥胖学生中男生不少于女生的概率.
已知数列 满足:
满足: ,
,
(Ⅰ) 求证:数列 是等差数列并求
是等差数列并求 的通项公式;
的通项公式;
(Ⅱ) 设 ,求证:
,求证: .
.
受日月引力的作用,海水会发生涨落,这种现象叫潮汐. 在通常情况下,船在海水涨潮时驶进航道,靠近码头,卸货后返回海洋.某港口水的深度 是时间
是时间 ,单位:
,单位: 的函数,记作:
的函数,记作: ,下表是该港口在某季每天水深的数据:
,下表是该港口在某季每天水深的数据:
经过长期观察 的曲线可以近似地看做函数
的曲线可以近似地看做函数 的图象.
的图象.
(Ⅰ)根据以上数据,求出函数 的近似表达式;
的近似表达式;
(Ⅱ)一般情况下,船舶航行时船底离海底的距离为 以上时认为是安全的(船舶停靠时,船底只需不碰到海底即可),某船吃水深度(船底离水面的距离)为
以上时认为是安全的(船舶停靠时,船底只需不碰到海底即可),某船吃水深度(船底离水面的距离)为 ,如果该船想在同一天内安全进出港,问它至多能在港内停留多长时间(忽略进出港所需时间)?
,如果该船想在同一天内安全进出港,问它至多能在港内停留多长时间(忽略进出港所需时间)?
如图所示,四棱锥 ,底面
,底面 是边长为
是边长为 的正方形,
的正方形, ⊥面
⊥面 ,
, ,过点
,过点 作
作 ,连接
,连接 .
.
(Ⅰ)求证: ;
;
(Ⅱ)若面 交侧棱
交侧棱 于点
于点 ,求多面体
,求多面体 的体积.
的体积.
已知 在
在 与
与 处都取得极值.
处都取得极值.
(Ⅰ) 求 ,
, 的值;
的值;
(Ⅱ)设函数 ,若对任意的
,若对任意的 ,总存在
,总存在 ,使得、
,使得、 ,求实数
,求实数 的取值范围.
的取值范围.
在平面直角坐标系 中,已知椭圆
中,已知椭圆 的左焦点为
的左焦点为 ,左、右顶点分别为
,左、右顶点分别为 ,上顶点为
,上顶点为 ,过
,过 三点作圆
三点作圆
(Ⅰ)若线段 是圆
是圆 的直径,求椭圆的离心率;
的直径,求椭圆的离心率;
(Ⅱ)若圆 的圆心在直线
的圆心在直线 上,求椭圆的方程;
上,求椭圆的方程;
(Ⅲ)若直线 交(Ⅱ)中椭圆于
交(Ⅱ)中椭圆于 ,交
,交 轴于
轴于 ,求
,求 的最大值
的最大值