已知全集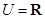 ,集合
,集合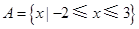 ,
,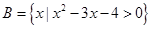 ,那么
,那么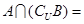 ( )
( )
A.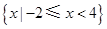 |
B.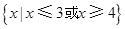 |
C.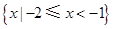 |
D.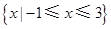 |
函数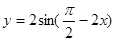 是( )
是( )
A.最小正周期为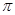 的偶函数 的偶函数 |
B.最小正周期为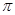 的奇函数 的奇函数 |
C.最小正周期为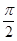 的偶函数 的偶函数 |
D.最小正周期为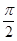 的奇函数 的奇函数 |
已知命题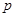 :
: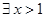 ,
,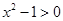 ,那么
,那么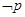 是( )
是( )
A.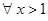 , ,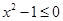 |
B.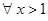 , ,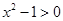 |
C.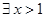 , ,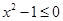 |
D.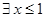 , ,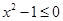 |
已知 是虚数单位,则复数
是虚数单位,则复数 的虚部为( )
的虚部为( )
A. |
B. |
C. |
D. |
右图是一个几何体的三视图,根据图中数据,可得该几何体的体积是( )
A. |
B. |
C. |
D. |

设变量 满足约束条件:
满足约束条件: ,则
,则 的( )
的( )
最小值为
A. |
B. |
C. |
D. |
已知数列 的前
的前 项和
项和 ,则
,则 =( )
=( )
| A.36 | B.35 | C.34 | D.33 |
在 中,角
中,角 所对的边分别为
所对的边分别为 ,若
,若 ,
, ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
若右边的程序框图输出的 是126,则条件①可为( )
是126,则条件①可为( )
A. |
B. |
C. |
D. |

椭圆 =1的左右焦点分别为
=1的左右焦点分别为 、
、 ,点
,点 是椭圆上任意一点,则
是椭圆上任意一点,则 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
设平面向量 ,则
,则 .
.
若直线 与幂函数
与幂函数 的图象相切于点
的图象相切于点
 ,则直线
,则直线 的方程为 .
的方程为 .
已知函数 ,则
,则 .
.
在极坐标系中,设曲线 与
与 的交点分别为
的交点分别为 ,则线段
,则线段 的垂直平分线的极坐标方程为 .
的垂直平分线的极坐标方程为 .
如图,从圆 外一点
外一点 引圆的切线
引圆的切线 和割线
和割线 ,已知
,已知 ,
, ,圆
,圆 的半径为
的半径为 ,则圆心
,则圆心 到直线
到直线 的距离为 .
的距离为 .
已知平面直角坐标系上的三点 ,
, ,
, (
( ),
), 为坐标原点,向量
为坐标原点,向量 与向量
与向量 共线.
共线.
(1)求 的值;
的值;
(2)求 的值.
的值.
某小组共有 五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)如下表所示:
五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)如下表所示:
| |
A |
B |
C |
D |
E |
| 身高 |
1.69 |
1.73 |
1.75 |
1.79 |
1.82 |
| 体重指标 |
19.2 |
25.1 |
18.5 |
23.3 |
20.9 |
(1)从该小组身高低于1.80的同学中任选2人,求选到的2人身高都在1.78以下的概率;
(2)从该小组同学中任选2人,求选到的2人的身高都在1.70以上且体重指标都在[18.5,23.9)中的概率.
如图,在底面为平行四边形的四棱柱 中,
中,
 底面
底面 ,
, ,
, ,
, .
.
(1)求证:平面 平面
平面 ;
;
(2)若 ,求四棱锥
,求四棱锥 的体积.
的体积.
设 是各项都为正数的等比数列,
是各项都为正数的等比数列,  是等差数列,且
是等差数列,且 ,
, ,
, .
.
(1)求数列 ,
, 的通项公式;
的通项公式;
(2)设数列 的前
的前 项和为
项和为 ,求数列
,求数列 的前
的前 项和
项和 .
.
已知抛物线 与双曲线
与双曲线 有公共焦点
有公共焦点 ,点
,点 是曲线
是曲线 在第一象限的交点,且
在第一象限的交点,且 .
.
(1)求双曲线 的方程;
的方程;
(2)以双曲线 的另一焦点
的另一焦点 为圆心的圆
为圆心的圆 与直线
与直线 相切,圆
相切,圆 :
: .过点
.过点 作互相垂直且分别与圆
作互相垂直且分别与圆 、圆
、圆 相交的直线
相交的直线 和
和 ,设
,设 被圆
被圆 截得的弦长为
截得的弦长为 ,
, 被圆
被圆 截得的弦长为
截得的弦长为 ,问:
,问: 是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
已知 为函数
为函数 图象上一点,O为坐标原点,记直线
图象上一点,O为坐标原点,记直线 的斜率
的斜率 .
.
(1)若函数 在区间
在区间
 上存在极值,求实数m的取值范围;
上存在极值,求实数m的取值范围;
(2)当  时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)求证: .
.