已知集合 则 ( )
则 ( )
A. |
B. |
C. |
D. |
复数 在复平面上对应的点位于 ( )
在复平面上对应的点位于 ( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
已知平面向量
 ,
,
 ,且
,且 ,则向量
,则向量 ( )
( )
A. |
B. |
C. |
D. |
已知直线 与直线
与直线
 平行且与圆:
平行且与圆: 相切,则直线
相切,则直线 的方程是( )
的方程是( )
A. |
B. 或 或 |
C. |
D. 或 或 |
对于平面 、
、 、
、 和直线
和直线 、
、 、
、 、
、 ,下列命题中真命题是( )
,下列命题中真命题是( )
A.若 ,则 ,则 |
B.若 ,则 ,则 |
C.若 则 则 |
D.若 ,则 ,则 |
不等式组 表示的平面区域的面积是( )
表示的平面区域的面积是( )
A. |
B.0 | C. |
D. |
已知函数 ,若过点
,若过点 且与曲线
且与曲线 相切的切线方程为
相切的切线方程为 ,则实数
,则实数 的值是( )
的值是( )
A. |
B. |
C.6 | D.9 |
对于任意两个正整数m, n , 定义某种运算“※”如下:当m ,n都为正偶数或正奇数时, ※
※ =
= 当
当 中一个为正偶数,另一个为正奇数时,
中一个为正偶数,另一个为正奇数时, ※
※ =
= .则在此定义下,集合
.则在此定义下,集合 ※
※ 中的元素个数是( )
中的元素个数是( )
| A.10个 | B.15个 | C.16个 | D.18个 |
右图是某高三学生进入高中三年来第 次到
次到 次的数学考试成绩茎叶图, 根据茎叶图计算数据的中位数为 .
次的数学考试成绩茎叶图, 根据茎叶图计算数据的中位数为 .
已知等差数列{ },满足
},满足 ,则此数列的前
,则此数列的前 项的和
项的和 .
.
已知直线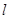 与直线
与直线 垂直,则直线
垂直,则直线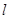 的倾斜角
的倾斜角 .
.
设 是
是 上的奇函数,
上的奇函数, . 当
. 当 时有
时有 ,则
,则 .
.
一物体在力 (单位:
(单位: )的作用下沿与力
)的作用下沿与力 相同的方向,从
相同的方向,从 处运动到
处运动到 (单位:
(单位: )处,则力
)处,则力 做的功为 焦.
做的功为 焦.
(坐标系与参数方程选做题)在极坐标系中,圆 的圆心到直线
的圆心到直线 的距离是 .
的距离是 .
如图, 为圆
为圆 直径,
直径, 切圆
切圆 于点
于点 ,
, ,
,  ,则
,则 等于 .
等于 .
已知函数 .(1)求
.(1)求 的最大值和最小正周期;(2) 若
的最大值和最小正周期;(2) 若 ,
, 是第二象限的角,求
是第二象限的角,求 .
.
某社团组织 名志愿者利用周末和节假日参加社会公益活动,活动内容是:1、到各社区宣传慰问,倡导文明新风;2、到指定的医院、福利院做义工,帮助那些需要帮助的人.各位志愿者根据各自的实际情况,选择了不同的活动项目,相关的数据如下表所示:
名志愿者利用周末和节假日参加社会公益活动,活动内容是:1、到各社区宣传慰问,倡导文明新风;2、到指定的医院、福利院做义工,帮助那些需要帮助的人.各位志愿者根据各自的实际情况,选择了不同的活动项目,相关的数据如下表所示:
| |
宣传慰问 |
义工 |
总计 |
| 20至40岁 |
11 |
16 |
27 |
| 大于40岁 |
15 |
8 |
23 |
| 总计 |
26 |
24 |
50 |
(1) 分层抽样方法在做义工的志愿者中随机抽取6名,年龄大于40岁的应该抽取几名?
(2) 上述抽取的6名志愿者中任取2名,求选到的志愿者年龄大于40岁的人数的数学期望.
如图,已知三棱锥 的侧棱
的侧棱 两两垂直,且
两两垂直,且 ,
, ,
, 是
是 的中点.(1)求
的中点.(1)求 点到面
点到面 的距离;(2)求二面角
的距离;(2)求二面角 的正弦值.
的正弦值.
已知等差数列 的公差
的公差 ,它的前
,它的前 项和为
项和为 ,若
,若 ,且
,且 成等比数列.(1) 求数列
成等比数列.(1) 求数列 的通项公式;(2)设数列
的通项公式;(2)设数列 的前
的前 项和为
项和为 ,求证:
,求证: .
.
在平面直角坐标系 中,点
中,点 为动点,
为动点, 分别为椭圆
分别为椭圆 的左右焦点.已知△
的左右焦点.已知△ 为等腰三角形.(1)求椭圆的离心率
为等腰三角形.(1)求椭圆的离心率 ;(2)设直线
;(2)设直线 与椭圆相交于
与椭圆相交于 两点,
两点, 是直线
是直线 上的点,满足
上的点,满足 ,求点
,求点 的轨迹方程.
的轨迹方程.
已知二次函数 ,且不等式
,且不等式 的解集为
的解集为 .
.
(1)方程 有两个相等的实根,求
有两个相等的实根,求 的解析式;
的解析式;
(2) 的最小值不大于
的最小值不大于 ,求实数
,求实数 的取值范围;
的取值范围;
(3) 如何取值时,函数
如何取值时,函数 存在零点,并求出零点.
存在零点,并求出零点.