空间两条直线 、
、 与直线
与直线 都成异面直线,则
都成异面直线,则 、
、 的位置关系是( )
的位置关系是( )
| A.平行或相交 | B.异面或平行 | C.异面或相交 | D.平行或异面或相交 |
已知 ,则
,则 等于( )
等于( )
A. |
B. |
C.8 | D.9 |
设函数 ,则
,则 的值为( )
的值为( )
A. |
B.0 | C.1 | D.5 |
某班级要从4名男生、2名女生中选4人接受心理调查,如果要求至少有1名女生,那么不同的选法种数为( )
| A.14 | B.24 | C.28 | D.48 |
某人练习射击,每次击中目标的概率为0.6,则他在五次射击中恰有四次击中目标的概率为( )
A. |
B. |
C. |
D. |
已知直线 ⊥平面
⊥平面 ,直线
,直线
 平面
平面 ,给出下列四个命题:
,给出下列四个命题:
① ②
② ③
③ ④
④
其中正确的命题是( )
| A.①② | B.③④ | C.②④ | D.①③ |
.如果 的展开式中含有非零常数项,则正整数
的展开式中含有非零常数项,则正整数 的最小值为( )
的最小值为( )
| A.5 | B.6 | C.7 | D.8 |
在正方体上任选3个顶点连成三角形,则所得的三角形是等边三角形的概率为( )
A. |
B. |
C. |
D. |
设 是函数
是函数 的导函数,
的导函数, 的图象如图1所示,
的图象如图1所示,
则 的图象最有可能的是( )
的图象最有可能的是( )
 |

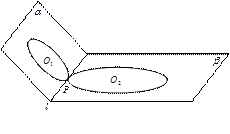
如图2,在 的二面角
的二面角 内,半径为1的圆
内,半径为1的圆
与半径为2的圆 分别在半平面
分别在半平面 、
、 内,且与棱
内,且与棱 切于
切于
同一点 ,则以圆
,则以圆 与圆
与圆 为截面的球的表面积为( )
为截面的球的表面积为( )
A. |
B.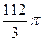 |
C.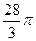 |
D. |
 的展开式中含
的展开式中含 项的系数为 。
项的系数为 。
记者要为4名奥运志愿者和他们帮助的2名外国友人拍照,要求排成一排,2名外国友人
不相邻且不排在两端,则不同的排法共有 种。(用数字作答)
设两个独立事件 和
和 都不发生的概率为
都不发生的概率为 ,
, 发生
发生 不发生的概率与
不发生的概率与 发生
发生 不发生
不发生
的概率相同,则事件 发生的概率
发生的概率 为 。
为 。
.如图3,在长方体 中,
中,  ,
, ,则
,则 与平面
与平面
所成角的正弦值为 。
 |
设函数 ,
, 有大于零的极值点,则
有大于零的极值点,则 的取值范围是 。
的取值范围是 。
(本小题满分13分)如图,正三棱柱 的所有棱长都为2,
的所有棱长都为2, 为
为 的中点。
的中点。
(Ⅰ)求证: ∥平面
∥平面 ;
;
(Ⅱ)求异面直线 与
与 所成的角。
所成的角。 
(本小题满分13分)已知 的展开式中,名项系数的和与其各项二项式系数的和之比为32
的展开式中,名项系数的和与其各项二项式系数的和之比为32
(Ⅰ)求
(Ⅱ)求展开式中二项式系数最大的项

(本小题满分13分)已知函数 处取得极值,并且它的图象
处取得极值,并且它的图象
与直线 在点(1,0)处相切。
在点(1,0)处相切。
(Ⅰ)求 、
、 、
、 的值;
的值;
(Ⅱ)求函数 的单调区间。
的单调区间。
(本小题满分12分)甲、乙两人进行一种游戏,两人同时随机地喊出杠、虎、鸡、虫,按照
杠打虎、虎吃鸡、鸡吃虫、虫啃杠的原则决定胜负。 (比如甲喊杠的同时,乙若喊虎则乙输,乙若
喊虫则乙赢,乙若喊杠或鸡则不分胜负。) 若两人同时喊出一次后不分胜负则继续喊下去,直到
分出胜负。
(Ⅰ)喊一次甲就获胜的概率是多少?
(Ⅱ)甲在喊不超过三次的情况下就获胜的概率是多少?
(本小题满分12分)如图,已知四棱锥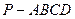 ,底面
,底面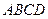 为菱形,
为菱形, ⊥平面
⊥平面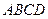 ,
, ,
, 、
、 分别是
分别是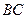 、
、 的中点。
的中点。
(Ⅰ)证明: ⊥
⊥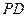 ;
;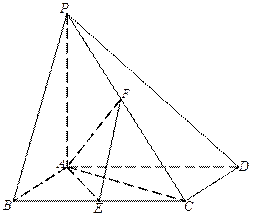 (Ⅱ)若
(Ⅱ)若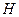 为
为 上的动点,
上的动点,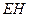 与平面
与平面 所成最大角的正切值为
所成最大角的正切值为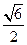 ,求二面角
,求二面角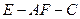 的余弦值。
的余弦值。
(本小题满分12分)已知函数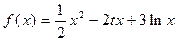 ,
,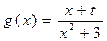 ,函数
,函数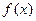
在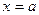 、
、 处取得极值,其中
处取得极值,其中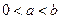 。
。
(Ⅰ)求实数 的取值范围;
的取值范围;
(Ⅱ)判断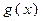 在
在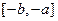 上的单调性;
上的单调性;
(Ⅲ)已知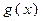 在
在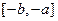 上的最大值比最小值大
上的最大值比最小值大  ,若方程
,若方程 有3个不同的解,
有3个不同的解,
求实数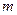 的取值范围。
的取值范围。