已知全集 ,集合
,集合 ,
,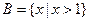 ,那么集合
,那么集合 =( )
=( )
A. |
B. |
C.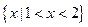 |
D. |
已知命题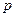 :
: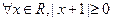 ,那么命题
,那么命题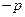 为( )
为( )
A.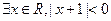 |
B.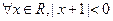 |
C.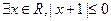 |
D.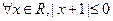 |
下列函数中,图象关于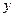 轴对称的是( )
轴对称的是( )
A. |
B.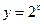 |
C. |
D.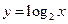 |
函数 的单调递减区间是( )
的单调递减区间是( )
A. |
B.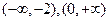 |
C.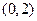 |
D.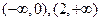 |
已知五个实数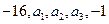 成等比数列,那么
成等比数列,那么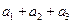 等于( )
等于( )
| A.—6或—14 | B.6或14 | C.—6或14 | D.6或—14 |
“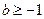 ”是“函数
”是“函数 为增函数”的( )
为增函数”的( )
| A.充分但不必要条件 | B.必要但不充分条件 |
| C.充要条件 | D.既不是充分条件也不是必要条件 |
数列 满足
满足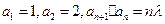 (
(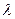 为常数,
为常数,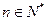 ),则
),则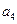 等于( )
等于( )
| A.1 | B.2 | C.3 | D.4 |
设集合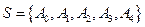 ,在集合
,在集合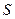 上定义运算
上定义运算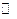 为:
为: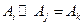 ,其中
,其中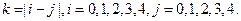 那么满足条件
那么满足条件
 的有序数对
的有序数对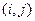 共有( )
共有( )
| A.16个 | B.12个 | C.8个 | D.6个 |
不等式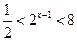 的解集是 .
的解集是 .
已知函数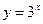 的反函数为
的反函数为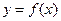 ,则
,则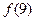 = .
= .
在等差数列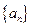 中,
中,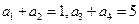 ,那么
,那么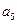 = .
= .
已知函数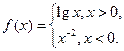 若
若 ,则
,则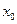 的值是 .
的值是 .
已知数列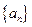 的前
的前 项和
项和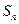 满足
满足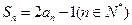 ,那么数列
,那么数列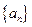 的通项公式为
的通项公式为 = .
= .
已知函数 的定义域是
的定义域是 ,对任意
,对任意 当
当 时,
时,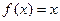 .关于函数
.关于函数 给出下列四个命题:
给出下列四个命题:
①函数 是奇函数;
是奇函数;
②函数 是周期函数;
是周期函数;
③函数 的全部零点为
的全部零点为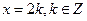 ;
;
④当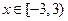 时,函数
时,函数 的图象与函数
的图象与函数 的图象有且只有三个公共点.其中全部真命题的序号是 .
的图象有且只有三个公共点.其中全部真命题的序号是 .
(本小题满分13分)
设等差数列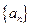 的前
的前 项和为
项和为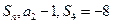 .
.
(I)求数列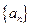 的通项公式;
的通项公式;
(II)若 ,求
,求 .
.
(本小题满分13分)
已知函数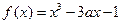 在
在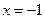 处取得极值.
处取得极值.
(I)求实数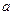 的值;
的值;
(II)当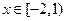 时,求函数
时,求函数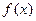 的值域.
的值域.
(本小题满分13分)
已知函数 ,其中
,其中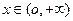 .
.
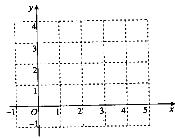
(I)在给定的坐标系中,画出函数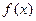 的图象;
的图象;
(II)设 ,且
,且 ,证明:
,证明: .
.
(本小题满分14分)
已知函数 .
.
(I)当 时,求曲线
时,求曲线 在点
在点 处切线的斜率;
处切线的斜率;
(II)当 时,求函数
时,求函数 的单调区间.
的单调区间.
(本小题满分14分)
从社会效益和经济效益出发,某地投入资金进行生态环境建设,并以此发展旅游产业.根据规划,第1年投入800万元,以后每年的投入将比上一年减少 ;当年旅游业收八为400万元,预计今后的旅游业收入每年会比上一年增加
;当年旅游业收八为400万元,预计今后的旅游业收入每年会比上一年增加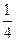 .
.
(I)设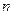 年的总投入为
年的总投入为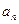 万元,旅游业总收入为
万元,旅游业总收入为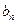 万元,写出
万元,写出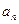 ,
,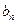 的表达式;
的表达式;
(II)至少经过多少年,旅游业的总收入才能超过总投入?(计算时取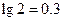 )
)
(本小题满分13分)
已知函数 ,其中
,其中 为自然对数的底数.
为自然对数的底数.
(I)求 的最小值;
的最小值;
(II)设 ,且
,且 ,证明:
,证明: .
.