若函数
,
(其中
)的最小正周期是
,且
,则( )
| A. |
|
B. |
|
| C. |
|
D. |
|
直线
关于直线
对称的直线方程是( )
| A. |
|
B. |
|
| C. |
|
D. |
|
要在边长为16米的正方形草坪上安装喷水龙头,使整个草坪都能喷洒到水.假设每个喷水龙头的喷洒范围都是半径为6米的圆面,则需安装这种喷水龙头的个数最少是( )

已知随机变量
服从正态分布
,
,则
=()
| A. |
|
| B. |
|
| C. |
|
| D. |
|
若
两条异面直线
外的任意一点,则()
| A. |
过点
有且仅有一条直线与
都平行 |
| B. |
过点
有且仅有一条直线与
都垂直 |
| C. |
过点
有且仅有一条直线与
都相交 |
| D. |
过点
有且仅有一条直线与
都异面 |
若非零向量
满足
,则()
| A. |
|
B. |
|
| C. |
|
D. |
|
设
是函数
的导函数,将
和
的图象画在同一个直角坐标系中,不可能正确的是( )
已知双曲线
的左、右焦点分别为
,
,
是准线上一点,且
,
,则双曲线的离心率是()
设
,
是二次函数,若
的值域是
,则
的值域是( )
| A. |
|
B. |
|
| C. |
|
D. |
|
已知复数
,则复数
.
已知
,且
,则
的值是.
不等式
的解集是.
某书店有11种杂志,2元1本的8种,1元1本的3种,小张用10元钱买杂志(每种至多买一本,10元钱刚好用完),则不同买法的种数是(用数字作答).
随机变量
的分布列如下:
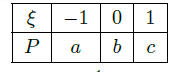
其中
成等差数列,若
,则
的值是 .
已知点
在二面角
的棱上,点
在
内,且
.若对于
内异于
的任意一点
,都有
,则二面角
的大小是 .
设
为实数,若
,则M的取值范围是.
已知
的周长为
,且
.
(I)求边
的长;
(II)若
的面积为
,求角
的度数.
在如图所示的几何体中,
平面
,
平面
,
,且
,
是
的中点.

(I)求证:
;
(II)求
与平面
所成的角.
如图,直线
与椭圆
交于
两点,记
的面积为
.

(I)求在
的条件下,
的最大值;
(II)当
时,求直线
的方程.
已知数列
中的相邻两项
,是关于 的方程
的两个根,且
.
的方程
的两个根,且
.
(I)求
,
,
,
;
(II)求数列
的前
项和
;
(Ⅲ)记
,
,
求证:
.
设
,对任意实数
,记
.
(I)求函数
的单调区间;
(II)求证:(ⅰ)当
时,
对任意正实数
成立;
(ⅱ)有且仅有一个正实数
,使得
对任意正实数
成立.

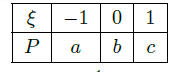


 的方程
的两个根,且
.
的方程
的两个根,且
.