设
均为直线,其中
在平面
的（ ）
| A．充分不必要条件 | B．必要不充分条件 |
| C．充分必要条件 | D．既不充分也不必要条件 |
.对于两个命题：
①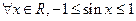
， ②
，
下列判断正确的是（ ）。
| A．① 假 ② 真 | B．① 真 ② 假 | C．① ② 都假 | D．① ② 都真 |
.与椭圆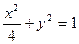
共焦点且过点
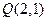的双曲线方程是（ ）
A． |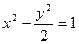
B． |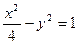
C． |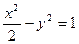
D． |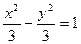
已知
是椭圆的两个焦点，过
且与椭圆长轴垂直的弦交椭圆与
,
两点，
则
是正三角形，则椭圆的离心率是（ ）
A 
B 
C 
D 
.过抛物线
的焦点作倾斜角为
直线
，直线与抛物线相交与
，
两点，则弦
的长是（ ）
A 8 B 16 C 32 D 64
在同一坐标系中，方程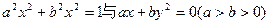
的曲线大致是（ ）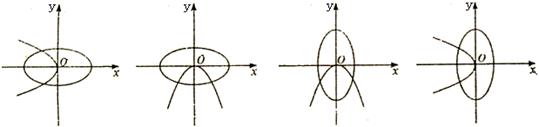
A． B． C． D．
已知椭圆
(
>0)的两个焦点F1，F2，点
在椭圆上，则
的面积最大值一定是（ ）
A 
B 
C 
D 
已知向量
互相垂直,则实数k的值是( )
| A．1 | B． |
C． |
D． |
在正方体
中，
是棱
的中点，则
与
所成角的余弦值为（ ）
A． |
B． |
C． |
D． |
.若椭圆
交于A，B两点,过原点与线段AB中点的连线的斜率为
，则
的值是( )
过抛物线
的焦点F作直线交抛物线于
两点，若
，则
的值为 （ ）
| A．5 | B．6 | C．8 | D．10 |
.以
=1的焦点为顶点，顶点为焦点的椭圆方程为 （ ）
A.
B. 
C. 
D.
已知A、B、C三点不共线，对平面ABC外一点O，给出下列表达式：
其中x，y是实数，若点M与A、B、C四点共面，则x+y=___
斜率为1的直线经过抛物线y2＝4x的焦点，且与抛物线相交于A,B两点，则
等于___
若命题P：“
x＞0，
”是真命题，则实数a的取值范围是___．
已知
，
为空间中一点，且
，则直线
与平面
所成角的正弦值为___．
（本小题满分1４）
设命题
：
，命题
：
；
如果“或”为真，“且”为假，求
的取值范围。
如图①在直角梯形ABCP中，BC∥AP，AB⊥BC，CD⊥AP，AD=DC=PD=2，E，F，G分别是线段PC、PD，BC的中点，现将ΔPDC折起，使平面PDC⊥平面ABCD（如图②）
（Ⅰ）求证AP∥平面EFG；
（Ⅱ）求二面角G-EF-D的大小；
（Ⅲ）在线段PB上确定一点Q，使PC⊥平面ADQ，试给出证
明．
(1５分) 如图，金砂公园有一块边长为2的等边△ABC的边角地，现修成草坪，图中DE把草坪
分成面积相等的两部分，D在AB上，E在AC上.
（Ⅰ）设AD＝
，DE＝
，求关于的函数关系式；
（Ⅱ）如果DE是灌溉水管，我们希望它最短，则DE的位置应在哪里？请予以证明.
（本小题满分1５分）
设
分别为椭圆
的左、右两个焦点.
（Ⅰ）若椭圆
上的点
两点的距离之和等于4，
求椭圆的方程和焦点坐标；
（Ⅱ）设点P是（Ⅰ）中所得椭圆上的动点，
。
（本小题满分1５分）
如图，设抛物线C：
的焦点为F，
为抛物线上的任一点（其中
≠0），[
过P点的切线交
轴于Q点．
（Ⅰ）证明：
；
（Ⅱ）Q点关于原点O的对称点为M，过M点作平行于PQ的直线
交抛物线C于A、B两点，若
，求
的值．