已知命题  R,
R, ,则 ( )
,则 ( )
A. R, R,  |
B. R, R,  |
C. R, R,  |
D. R, R,  |
“p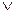 q为真”是“
q为真”是“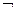 p为假”的 ( )
p为假”的 ( )
| A.充分不必要条件. | B.必要不充分条件 |
C.充要条件 |
D.既不充分也不必要条件 |
“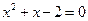 ”成立的一个充分而不必要条件是 ( )
”成立的一个充分而不必要条件是 ( )
A.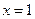 . . |
B.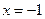 . . |
C.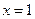 或 或 . . |
D.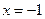 或 或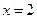 . . |
曲线 在点
在点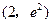 处的切线与坐标轴所围三角形的面积为 ( )
处的切线与坐标轴所围三角形的面积为 ( )
A.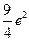 |
B.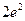 |
C.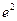 |
D.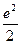 |
椭圆的焦距为2,则m的值等于 ( )
| A.5或3 | B.8 | C.5 | D. |
设甲、乙、丙、丁是四个命题,甲是乙的充分而不必要条件,丙是乙的充要条件,丁是丙的必要而不充分条件,那么丁是甲的 ( )
| A.充分不必要条件. | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知P是双曲线 上一点,双曲线的一条渐近线方程为3x-
上一点,双曲线的一条渐近线方程为3x- 2y=0,F1 、F2分别是双曲线的左、右焦点,若|P F1 |=3,则|P F2|=" " ( )
2y=0,F1 、F2分别是双曲线的左、右焦点,若|P F1 |=3,则|P F2|=" " ( )
| A.7 | B.6 | C.5 | D.3 |
△ABC一边的两个顶点为B( 3,0),C(3,0)另两边所在直线的斜率之积为
3,0),C(3,0)另两边所在直线的斜率之积为 (
( 为常数),则顶点A的轨迹不可能落在下列哪一种曲线上 ( )
为常数),则顶点A的轨迹不可能落在下列哪一种曲线上 ( )
| A.圆 | B.椭圆 | C.双曲线 | D.抛物线 |
设 是函数
是函数 的导函数
的导函数 ,将
,将 和
和 的图象画在同一个直角坐标系中,不可能正确的是 ( )
的图象画在同一个直角坐标系中,不可能正确的是 ( )
已知曲线C: ,直线
,直线 ,当
,当 时,直线
时,直线 恒在曲线C的上方,则实数
恒在曲线C的上方,则实数 的取值范围是 ( )
的取值范围是 ( )
A. |
B. |
C. |
D. |
设偶函数f(x)=loga|ax+b|在(0,+∞)上单调递增,
则f(b-2)与f(a+1)的大小关系是( )
A.f(b-2)= f(a+1)
f(a+1) B
B .f(b-2)>f(a+1)
.f(b-2)>f(a+1)  C.f(b-2)<f(a+1) D.不能确定
C.f(b-2)<f(a+1) D.不能确定
定义 的运算分别对应下图中的(1)、(2)、(3)、(4),那么下图中的(A)、(B)所对应的运算结果可能是( )
的运算分别对应下图中的(1)、(2)、(3)、(4),那么下图中的(A)、(B)所对应的运算结果可能是( )
(1) (2) (3) (4) (A) (B)
A、 B、
B、
C、 D、
D、
数列 中的第10项是 。
中的第10项是 。
在ΔABC中,若sinA:sinB:s inC=5:7:8,则∠B的大小是 。
inC=5:7:8,则∠B的大小是 。
已知 =
= ,则不等式
,则不等式 的解集是 。
的解集是 。
与圆 相切且在两坐标轴上截距相等的直线方程 。
相切且在两坐标轴上截距相等的直线方程 。
(本小题满分10分) 已知等差数列前三项为
已知等差数列前三项为 ,4,3
,4,3 ,前
,前 项和
项和 ,若
,若 =2550。
=2550。
(1) 求 及
及 的值;(2)求
的值;(2)求 。
。
(本小题满分12分)
已知函数 ,
,
(1)求 的在定义域;
的在定义域;
(2)讨论 的单调性;(不要求证明)
的单调性;(不要求证明)
(3)求 的反函数
的反函数 。
。
(本小题满分12分)
已知函数 的图象在
的图象在 轴右侧的第一个最高点(函数取最大值的点)为
轴右侧的第一个最高点(函数取最大值的点)为 ,与
,与 轴在原点右侧的第一个交点为N(6,0),求这个函数的解析式。
轴在原点右侧的第一个交点为N(6,0),求这个函数的解析式。
(本小题满分12分)
椭圆 的离心率是
的离心率是 ,求椭圆两准线间的距离。
,求椭圆两准线间的距离。
(本小题满分12分)
如图,已知ABCD是矩形,PD⊥平面ABCD,PB=2,PB与平面ABCD所成的角为30º,PB与平面PCD所成的角为45º,求:
(1)PB与CD所成角的大小;
(2)二 面角C—PB—D的大小。
面角C—PB—D的大小。

(本小题满分12分)
在某种考试中,设A、B、C三人考中的概率分别是 、
、 、
、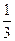 ,且各自考中的事件是相互独立的。
,且各自考中的事件是相互独立的。
(1)求3人都考中的概率;
(2)求只有2人考中的概率;
(3)几人考中的事件最容易发生?