圆x2+y2-2x+4y-4=0的圆心坐标是( )
| A.(-2,4) | B.(2,-4) | C.(-1,2) | D.(1,-2) |
如果AC<0,BC<0,那么直线Ax+By+C=0不通过( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
已知等差数列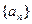 的前n项和为Sn,若
的前n项和为Sn,若 等于( )
等于( )
| A.18 | B.36 | C.54 | D.72 |
在空间坐标中,点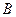 是
是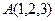 在
在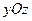 坐标平面内的射影,O为坐标原点,则
坐标平面内的射影,O为坐标原点,则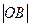 等于( )
等于( )
A.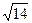 |
B.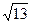 |
C.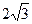 |
D.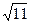 |
已知直线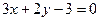 和
和 互相平行,则它们之间的距离是( )
互相平行,则它们之间的距离是( )
| A.4 | B. |
C.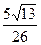 |
D.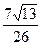 |
如图,正方体ABCD-A1B1C1D1中,M、N、P、Q分别是AB、BC、CD、C1C的中点,直线MN与PQ所成的角的度数是( )
A.45o B.60o C.30o D.90o
已知圆 :
: 及直线
及直线 ,当直线
,当直线 被
被 截得的弦长为
截得的弦长为 时,则
时,则 ( )
( )
A. |
B. |
C. |
D. |
三棱锥的三条侧棱两两垂直,则顶点在底面的射影是底面三角形的( )
| A.垂心 | B.内心 | C.外心 | D.重心 |
帐篷是重要的救灾物资。某种帐篷的







 三视图如图(单位:m),那么生产这 1
三视图如图(单位:m),那么生产这 1




 样一顶帐篷大约需要篷布
样一顶帐篷大约需要篷布
 2
2

 正视图 侧视图
正视图 侧视图 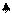











A.50 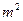 |
B.52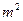 2 2 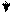      |
C.54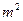 |
D.60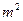 2 2 |

 4
4
俯视图
如果实数x、y满足条件 ,若
,若 有最大值时的
有最大值时的 满足
满足 (
( >0,
>0,  >0),则
>0),则 的最小值为( )
的最小值为( )
| A.4 | B. |
C. |
D.5 |
数列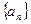 的前n项的和
的前n项的和 ,则此数列的通项公式
,则此数列的通项公式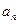 =
=
过点(1,2)且在两坐标轴上的截距相等的直线的方程 ;
设 为圆
为圆 上一动点,则
上一动点,则 到直线
到直线 的最大距离是 。
的最大距离是 。
过原点O作圆x2+y2-8x=0的弦OA,则弦OA中点M的轨迹方程是 .
(本小题满分10分)在等差数列 中,
中, ,
, 。
。
(1) 求数列 的通项公式;
的通项公式;
(2) 令 ,求数列
,求数列 的前
的前 项和
项和
(本小题满分10分)在△ABC中,内角A,B,C的对边分别为a,b,c,
已知a,b,c成等比数列,且  .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)设 的值。
的值。
(本小题满分10分)如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E、F分别是AB、SC的中点。
(Ⅰ)求证:EF∥平面SAD;
(Ⅱ)设SD=2CD,求二面角A-EF-D的正切值;
(本小题满分10分)某食品厂定期购买面粉,已知该厂每天需用面粉6吨,每吨面粉的价格为1800元,面粉的保管等其他费用为平均每吨3元,购面粉每次需支付运费900元。
(1)求该厂多少天购买一次面粉,才能使平均每天所支付的总费用最少?
(2)若提供面粉的公司规定:当一次购买面粉不少于210吨时,其价格可享受九折优惠,问该厂是否考虑利用此优惠条件?请说明理由。
(本小题满分10分)已知圆C的圆心在直线y=x+1上,且过点A(1,3),与直线x+2y-7=0相切.
(1)求圆C的方程;
(2)设直线 :
:
 与圆C相交于A、B两点,求实数
与圆C相交于A、B两点,求实数 的取值范围;
的取值范围;
(3)在(Ⅱ)的条件下,是否存在实数 ,使得弦
,使得弦 的垂直平分线
的垂直平分线 过点
过点 , 若存在,求出实数
, 若存在,求出实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. 