已知复数
满足
,则复数的共轭复数为( )
A． |
B． |
C． |
D． |
设
,已知集合
，
，且
，则实数
的取值范围是（ ）
A． |
B． |
C． |
D． |
已知点
，
，则与
共线的单位向量为（ ）
A． 或 |
B． |
C． 或 |
D． |
已知
，则
（ ）
A． |
B． |
C． |
D． |
执行右面的程序框图，那么输出
的值为（ ）
| A．9 | B．10 | C．45 | D．55 |
设等差数列
的前
项和为
，且
，
，则
（ ）
| A．90 | B．100 | C．110 | D．120 |
某几何体的三视图如图所示，则它的侧面积为（ ）
A． |
B． |
C．24 | D． |
已知双曲线
的左、右焦点分别为
，以
为直径的圆与双曲线渐近线的一个交点为
，则此双曲线的方程为（ ）
A． |
B． |
C． |
D． |
直三棱柱
的六个顶点都在球
的球面上，若
，
，
，则球的表面积为（ ）
A． |
B． |
C． |
D． |
设函数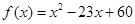
，
，则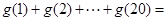
（ ）
| A．0 | B．38 | C．56 | D．112 |
在长度为3的线段上随机取两点，将其分成三条线段，则恰有两条线段的长大于1的概率为（ ）
A． |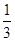
B． |
C． |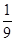
D． |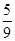
设
，则
的最小值为（ ）
| A．4 | B．16 | C．5 | D．25 |
过坐标原点与曲线
相切的直线方程为 .
抛物线
的准线截圆
所得弦长为2，则
= .
若存在正数
，使
成立，则实数
的取值范围是 .
已知数列
满足
，
，
，则的前
项和
= .
在
中，角
所对的边分别是
，已知
.
（Ⅰ）求
；
（Ⅱ）若
，且
，求的面积.
从某校高三上学期期末数学考试成绩中，随机抽取了60名学生的成绩得到频率分布直方图如下：
（Ⅰ）根据频率分布直方图，估计该校高三学生本次数学考试的平均分；
（Ⅱ）以上述样本的频率作为概率，从该校高三学生中有放回地抽取3人，记抽取的学生成绩不低于90分的人数为
，求的分布列和期望.
在如图所示的几何体中，四边形
均为全等的直角梯形，且
，
.
（Ⅰ）求证：
平面
；
（Ⅱ）求二面角
的余弦值.
已知点
是椭圆
：
上一点，
分别为的左右焦点
，
，
的面积为
.
（Ⅰ）求椭圆的方程；
（Ⅱ）设
，过点
作直线
，交椭圆异于
的
两点，直线
的斜率分别为
，证明：
为定值.
已知函数
.
（Ⅰ）讨论
的单调性；
（Ⅱ）若
恒成立，证明：当
时，
.
如图，
为圆
的直径，
为垂直于的一条弦，垂足为
，弦
与交于点
.
（Ⅰ）证明：
四点共圆；
（Ⅱ）证明：
.
极坐标系与直角坐标系
有相同的长度单位，以原点
为极点，以
轴正半轴为极轴.已知直线
的参数方程为
（
为参数），曲线
的极坐标方程为
.
（Ⅰ）求的直角坐标方程；
（Ⅱ）设直线与曲线交于
两点，求弦长
.
设函数
.
（Ⅰ）解不等式
；
（Ⅱ）若不等式
的解集为
，求实数
的取值范围.