复数
满足
（
为虚数单位），则的共轭复数
为 （ ）
A． |
B． |
C． |
D． |
已知集合
均为全集
的子集，且
,
,则
（ ）
A． |
B． |
C． |
D． |
已知等差数列
满足
， 
，则它的前10项和
（ ）
| A．85 | B．135 | C．95 | D．23 |
对于平面
，
，
和直线
，
，
，
，下列命题中真命题是 （ ）
A．若 ,则 ； |
B．若 则 ； |
C．若 ,则 ； |
D．若 ,则 . |
某程序框图如图所示，若该程序运行后输出的值是
，则 （ ）
A． |
B． |
C． |
D． |
将函数
的图像向右平移
个单位，那么所得的图像所对应的函数解析式是（ ）
A． |
B． |
C． |
D． |
给出下列四个结论：
①若命题
，则
；
② “
”是“
”的充分而不必要条件；
③命题“若
，则方程
有实数根”的逆否命题为：“若方程没有实数根，则
0”；
④若
，则
的最小值为
．
其中正确结论的个数为 （ ）
| A． |
B． |
C． |
D． |
已知函数
是定义在
上的奇函数，若对于任意的实数
，都有
，且当
时，
，则
的值为 （ ）
A． |
B． |
C． |
D． |
设二项式
的展开式中常数项为
,则
．
一物体在力
(单位：
)的作用下沿与力
相同的方向,从
处运动到
(单位：
)处,则力
做的功为 焦．
设
，其中实数
满足
，若
的最大值为
，则
.
已知双曲线
的两条渐近线与抛物线
的准线分别交于
两点，
为坐标原点．若双曲线的离心率为2,
的面积为
,则
.
在区间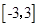
上随机取一个数
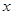，使得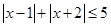
成立的概率为 ．
已知极坐标的极点与平面直角坐标系的原点重合，极轴与
轴的正半轴重合，且长度单位相同．圆
的参数方程为
为参数），点
的极坐标为（
，
）．若点
是圆上的任意一点，
两点间距离的最小值为 .
如图，
是⊙
的直径，
是延长线上的一点，过作⊙的切线，切点为
，
，若
，则⊙的直径
__________ ．
在
中，角
的对边分别为
向量
，
,且
．
（１）求
的值；
（２）若
,
,求角
的大小及向量
在
方向上的投影．
为了解甲、乙两厂产品的质量，从两厂生产的产品中分别随机抽取各10件样品，测量产品中某种元素的含量（单位：毫克）.如图是测量数据的茎叶图：
规定：当产品中的此种元素含量不小于18毫克时，该产品为优等品.
（1）试用上述样本数据估计甲、乙两厂生产的优等品率；
（2）从乙厂抽出的上述10件样品中，随机抽取3件，求抽到的3件样品中优等品数
的分布列及其数学期望
；
（3）从甲厂的10件样品中有放回的随机抽取3件，也从乙厂的10件样品中有放回的随机抽取3件，求抽到的优等品数甲厂恰比乙厂多2件的概率．
如图，在四棱锥
中，侧面
底面
,
,
为
中点，底面是直角梯形，
,
，
,
．
(1) 求证：
平面
；
(2) 求证：平面
平面
；
(3) 设
为棱上一点，
,试确定
的值使得二面角
为
．
若数列
的前
项和为
，对任意正整数都有
，记
．
（1）求
,
的值；
（2）求数列
的通项公式；
（3）若
求证：对任意
．
已知椭圆
：
的长轴长为4，且过点
．
（１）求椭圆的方程；
（２）设
、
、
是椭圆上的三点，若
，点
为线段
的中点，
、
两点的坐标分别为
、
，求证：
．
已知函数
．
（1）若
在
处取得极值，求
的值；
（2）求的单调区间；
（3）若
且
，函数
，若对于
，总存在
使得
，求实数
的取值范围．