已知全集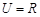 ,集合
,集合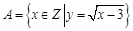
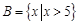 ,则
,则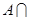
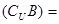 ( )
( )
A.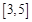 |
B.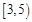 |
C.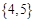 |
D. |
复数 的虚部为 ( )
的虚部为 ( )
| A.2 | B.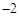 |
C.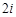 |
D.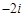 |
若焦点在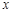 轴上的双曲线
轴上的双曲线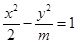 的离心率为
的离心率为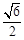 ,则该双曲线的渐近线方程为( )
,则该双曲线的渐近线方程为( )
A.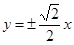 |
B.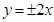 |
C.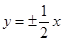 |
D.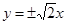 |
按照如图的程序运行,已知输入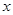 的值为2+log23,则输出
的值为2+log23,则输出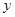 的值为 ( )
的值为 ( )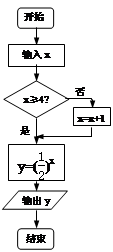
A.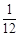 |
B.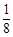 |
C.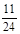 |
D.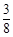 |
已知等比数列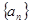 的首项
的首项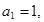 公比
公比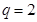 ,则
,则 ( )
( )
| A.50 | B.35 | C.55 | D.46 |
已知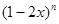 展开式中,奇数项的二项式系数之和为64,则
展开式中,奇数项的二项式系数之和为64,则 展开式中含
展开式中含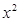 项的系数为 ( )
项的系数为 ( )
| A.71 | B.70 | C.21 | D.49 |
如图是一几何体的三视图,则该几何体的体积是 ( )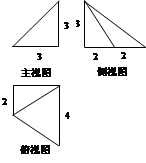
| A.9 | B.10 | C.12 | D.18 |
设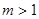 ,当实数
,当实数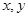 满足不等式组
满足不等式组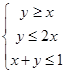 时,目标函数
时,目标函数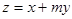 的最大值等于2,则
的最大值等于2,则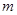 的值是( )
的值是( )
| A.2 | B.3 | C.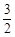 |
D.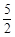 |
.已知函数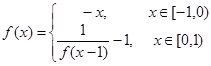 ,若方程
,若方程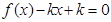 有两个实数根,则
有两个实数根,则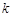 的取值范围是( )
的取值范围是( )
A.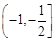 |
B.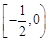 |
C.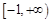 |
D.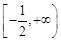 |
已知三棱锥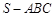 的所有顶点都在球
的所有顶点都在球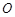 的球面上,
的球面上, 为球
为球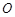 的直径,且
的直径,且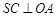 ,
,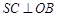 ,
,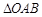 为等边三角形,三棱锥
为等边三角形,三棱锥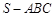 的体积为
的体积为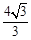 ,则球
,则球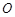 的半径为( )
的半径为( )
| A.3 | B. 1 | C.2 | D.4 |
抛物线 的焦点为
的焦点为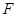 ,点
,点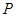 为抛物线上的动点,点
为抛物线上的动点,点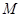 为其准线上的动点,当
为其准线上的动点,当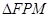 为等边三角形时,则
为等边三角形时,则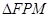 的外接圆的方程为( )
的外接圆的方程为( )
A.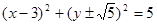 |
B.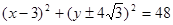 |
C.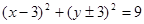 |
D. |
已知函数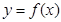 定义域为
定义域为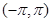 ,且函数
,且函数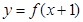 的图象关于直线
的图象关于直线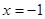 对称,当
对称,当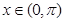 时,
时,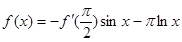 ,(其中
,(其中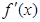 是
是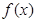 的导函数),若
的导函数),若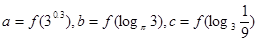 ,则
,则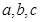 的大小关系是( )
的大小关系是( )
A.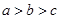 |
B.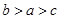 |
C.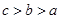 |
D.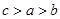 |
已知向量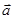 ,
,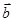 满足
满足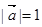 ,
,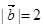 ,
,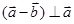 ,则向量
,则向量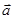 与向量
与向量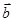 的夹角为 .
的夹角为 .
已知数列{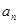 }满足
}满足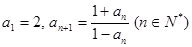 ,则
,则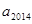 的值为 .
的值为 .
设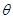 为第四象限角,
为第四象限角,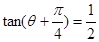 ,则
,则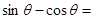 .
.
已知数列{ }的前
}的前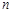 项和
项和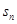 满足
满足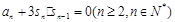 ,
, ,则
,则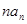 的最小值为 .
的最小值为 .
已知函数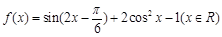 .
.
(1)求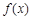 的单调递增区间;
的单调递增区间;
(2)在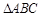 中,三内角
中,三内角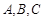 的对边分别为
的对边分别为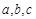 ,已知
,已知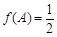 ,
,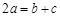 ,
,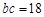 .求
.求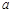 的值.
的值.
如图,四棱锥P-ABCD中, ,
,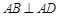 ,
,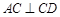 ,
,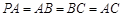 ,
,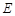 是
是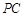 的中点.
的中点.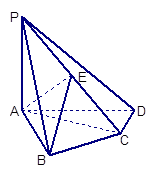
(1)求证: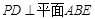 ;
;
(2)求二面角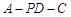 的平面角的正弦值.
的平面角的正弦值.
在一次数学考试中,第22,23,24题为选做题,规定每位考生必须且只须在其中选做一题,设5名考生选做这三题的任意一题的可能性均为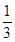 ,每位学生对每题的选择是相互独立的,各学生的选择相互之间没有影响.
,每位学生对每题的选择是相互独立的,各学生的选择相互之间没有影响.
(1)求其中甲、乙两人选做同一题的概率;
(2)设选做第23题的人数为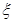 ,求
,求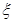 的分布列及数学期望.
的分布列及数学期望.
设椭圆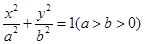 的左焦点为
的左焦点为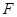 ,离心率为
,离心率为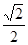 ,过点
,过点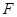 且与
且与 轴垂直的直线被椭圆截得的线段长为
轴垂直的直线被椭圆截得的线段长为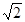 .
.
(1) 求椭圆方程.
(2) 过点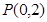 的直线
的直线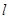 与椭圆交于不同的两点
与椭圆交于不同的两点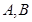 ,当
,当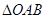 面积最大时,求
面积最大时,求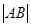 .
.
设函数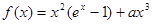
(1) 当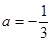 时,求
时,求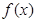 的单调区间;
的单调区间;
(2) 若当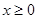 时,
时,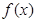
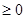 恒成立,求
恒成立,求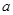 的取值范围.
的取值范围.
如图,直线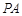 为圆
为圆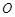 的切线,切点为
的切线,切点为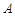 ,直径
,直径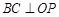 ,连接
,连接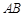 交
交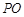 于点
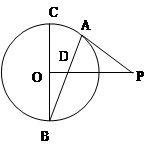
于点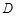 .
.
(Ⅰ)证明: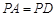 ;
;
(Ⅱ)求证: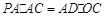 .
.
在平面直角坐标系中,以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线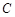 的极坐标方程为
的极坐标方程为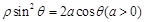 ,过点
,过点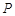 (-2,-4)的直线
(-2,-4)的直线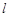 的参数方程为
的参数方程为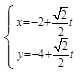 (
(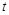 为参数),直线
为参数),直线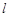 与曲线
与曲线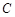 相交于
相交于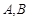 两点.
两点.
(Ⅰ)写出曲线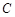 的直角坐标方程和直线
的直角坐标方程和直线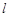 的普通方程;
的普通方程;
(Ⅱ)若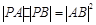 ,求
,求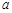 的值.
的值.
已知函数 .
.
(Ⅰ)求使不等式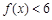 成立的
成立的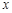 的取值范围;
的取值范围;
(Ⅱ)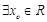 ,
, ,求实数
,求实数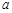 的取值范围.
的取值范围.