已知全集 ,集合
,集合 ,
, ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
已知命题 :
: ,则
,则 是( )
是( )
A. |
B. |
C. |
D. |
函数 是幂函数,且在
是幂函数,且在 上为增函数,则实数
上为增函数,则实数 的值是( )
的值是( )
A. |
B. |
C. |
D. 或 或 |
已知函数 是
是 上的单调增函数且为奇函数,数列
上的单调增函数且为奇函数,数列 是等差数列,
是等差数列, ,则
,则 的值( )
的值( )
| A.恒为正数 | B.恒为负数 |
| C.恒为0 | D.可以为正数也可以为负数 |
满足 ,且
,且 的集合
的集合 的个数是( )
的个数是( )
| A.1 | B.2 | C.3 | D.4 |
“ ”是“
”是“ ”的( )
”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
如图, 与圆
与圆 相切于点
相切于点 ,直线
,直线 交圆
交圆 于
于 两点,弦
两点,弦 垂直
垂直 于
于 .则下面结论中,错误的结论是( )
.则下面结论中,错误的结论是( )
A. ∽ ∽ |
B. |
C. |
D. |
函数 的单调递增区是( )
的单调递增区是( )
A. |
B. |
C. 和 和 |
D. |
已知函数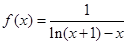 ,则
,则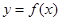 的图像大致为
的图像大致为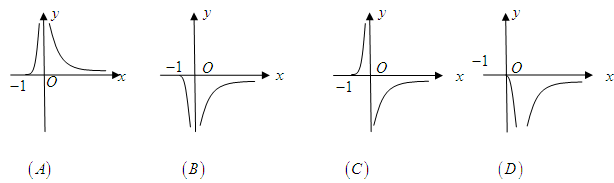
定义方程 的实数根
的实数根 叫做函数
叫做函数 的“新驻点”,若函数
的“新驻点”,若函数
 的“新驻点”分别为
的“新驻点”分别为 ,则
,则 的大小关系为( )
的大小关系为( )
A. |
B. |
C. |
D. |
已知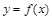 是定义在R上周期为4的奇函数,且
是定义在R上周期为4的奇函数,且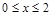 时,
时, 则
则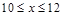 时,
时,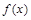 =_________________
=_________________
以直角坐标系的原点为极点,x轴的正半轴为极轴,并在两种坐标系中取相同的长度单位.已知直线的极坐标方程为 (
( ∈R),它与曲线
∈R),它与曲线 (
( 为参数)相交于两点A和B,则
为参数)相交于两点A和B,则 .
.
设二次函数 的值域为
的值域为 ,则
,则 的最大值为 .
的最大值为 .
设 .若曲线
.若曲线 与直线
与直线 所围成封闭图形的面积为
所围成封闭图形的面积为 ,则
,则 ______.
______.
函数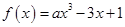 对于
对于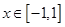 总有
总有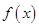 ≥0 成立,则
≥0 成立,则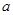 的取值集合为 .
的取值集合为 .
已知命题 :不等式
:不等式 的解集为R,命题
的解集为R,命题 :
: 是
是 上的增函数,若
上的增函数,若 或
或 为真命题,
为真命题, 且
且 为假命题,求实数
为假命题,求实数 的取值范围.
的取值范围.
已知 ,其中
,其中 ,如果A∩B=B,求实数
,如果A∩B=B,求实数 的取值范围.
的取值范围.
设函数 为奇函数,其图象在点
为奇函数,其图象在点 处的切线与直线
处的切线与直线 垂直,导函数
垂直,导函数 的最小值为
的最小值为 .
.
(1)求 的值;
的值;
(2)求函数 的单调递增区间,并求函数
的单调递增区间,并求函数 在
在 上的最大值和最小值.
上的最大值和最小值.
已函数 是定义在
是定义在 上的奇函数,在
上的奇函数,在 上
上 .
.
(1)求函数 的解析式;并判断
的解析式;并判断 在
在 上的单调性(不要求证明);
上的单调性(不要求证明);
(2)解不等式 .
.
预计某地区明年从年初开始的前 个月内,对某种商品的需求总量
个月内,对某种商品的需求总量 (万件)近似满足:
(万件)近似满足: N*,且
N*,且 )
)
(1)写出明年第 个月的需求量
个月的需求量 (万件)与月份
(万件)与月份 的函数关系式,并求出哪个月份的需求量超过
的函数关系式,并求出哪个月份的需求量超过 万件;
万件;
(2)如果将该商品每月都投放到该地区 万件(不包含积压商品),要保证每月都满足供应,
万件(不包含积压商品),要保证每月都满足供应, 应至少为多少万件?(积压商品转入下月继续销售)
应至少为多少万件?(积压商品转入下月继续销售)
已知函数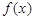 的定义域为
的定义域为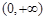 ,若
,若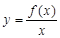 在
在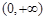 上为增函数,则称
上为增函数,则称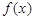 为“一阶比增函数”;若
为“一阶比增函数”;若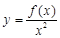 在
在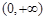 上为增函数,则称
上为增函数,则称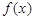 为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为
为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为 ,所有“二阶比增函数”组成的集合记为
,所有“二阶比增函数”组成的集合记为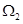 .
.
(Ⅰ)已知函数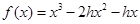 ,若
,若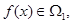 且
且 ,求实数
,求实数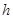 的取值范围;
的取值范围;
(Ⅱ)已知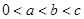 ,
,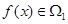 且
且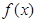 的部分函数值由下表给出,
的部分函数值由下表给出,
 |
 |
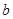 |
 |
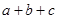 |
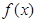 |
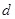 |
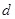 |
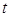 |
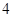 |
求证: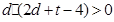 ;
;
(Ⅲ)定义集合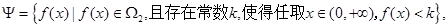
请问:是否存在常数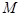 ,使得
,使得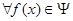 ,
,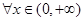 ,有
,有 成立?若存在,求出
成立?若存在,求出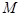 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.