若 是任意实数,且
是任意实数,且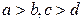 ,则 ( )
,则 ( )
A.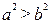 |
B. |
C.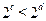 |
D. |
已知 成等差数列,
成等差数列,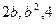 成等比数列,则
成等比数列,则 ( )
( )
| A.2 | B. |
C.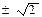 |
D. |
三鹿婴幼儿奶粉事件发生后,质检总局紧急开展了关于液态奶三聚氰胺的专项检查。假设蒙牛,伊利,光明三家公司生产的某批次液态奶分别是 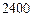 箱,
箱, 箱和
箱和 箱,现分层随机抽取
箱,现分层随机抽取 箱进行检验,则蒙牛、光明这两家公司生产的液态奶被抽取箱数之和为 ( )
箱进行检验,则蒙牛、光明这两家公司生产的液态奶被抽取箱数之和为 ( )
| A.300 | B.380 | C.320 | D.500 |
一枚硬币连掷 次,恰有两次正面朝上的概率是 ( )
次,恰有两次正面朝上的概率是 ( )
A.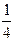 |
B.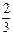 |
C. |
D.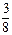 |
在 中,
中,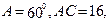 面积
面积 则
则 的长为 ( )
的长为 ( )
| A.75 | B.51 | C.49 | D. |
右图中,程序框图的循环体执行的次数是 ( )
| A.100 |
| B.99 |
| C.98 |
| D.97 |
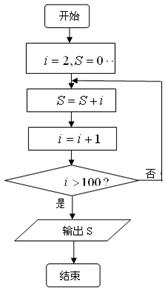
读算法,完成该题:第一步,李同学拿出一正方体;第二步,把正方体表面全涂上红色;第三步,将该正方体切割成27个全等的小正方体;第四步,将这些小正方体放到一箱子里,搅拌均匀;第五步,从箱子里随机取一个小正方体。问:取到的小正方体恰有三个面为红色的概率是 ( )
A.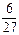 |
B.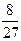 |
C.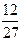 |
D.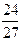 |
在 中,角
中,角 所对的边分别为
所对的边分别为 ,已知
,已知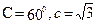 ,求使得ab取得最大值时的该三角形面积为 ( )
,求使得ab取得最大值时的该三角形面积为 ( )
A.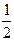 |
B. |
C.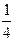 |
D.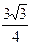 |
已知

 ,若向区域
,若向区域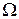 内随机投一点
内随机投一点 ,则点
,则点 落在区域
落在区域 内的概率为 ( )
内的概率为 ( )
A.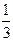 |
B. |
C. |
D. |
设 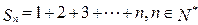 ,则
,则 的最大值.为( )
的最大值.为( )
A. |
B. |
C. | D. |
一个容量为 的样本分成若干组,已知某组的频数和频率分别为
的样本分成若干组,已知某组的频数和频率分别为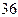 和
和 ,则
,则 _____.
_____.
若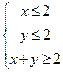 ,则目标函数
,则目标函数 的取值范围是_______________.
的取值范围是_______________.
设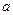 是甲随机抛掷一枚骰子得到的点数,则使方程
是甲随机抛掷一枚骰子得到的点数,则使方程 有两个不相等的实数根的概率为_______.
有两个不相等的实数根的概率为_______.
若 ,则不等式
,则不等式 的解集为________________.
的解集为________________.
已知数列 的前
的前 项和
项和 ,把数列
,把数列 的各项排成三角形形状如下:记第
的各项排成三角形形状如下:记第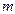 行第
行第 列上排的数为
列上排的数为 ,则
,则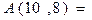 _____________.
_____________.
(满分9分)如图,已知梯形 中,
中,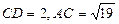 ,
,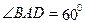 。求梯形的高.
。求梯形的高.
(满分10分)用自然语言设计一种计算 的值的算法,并画出相应的程序框图。
的值的算法,并画出相应的程序框图。
(满分9分)盒子中有大小形状相同的4只红球、2只黑球,每个球被摸到的机会均等,求下列事件的概率:
(1)A=“任取一球,得到红球”;
(2)B=“任取两球,得到同色球”;
(3)C=“任取三球,至多含一黑球”。
(满分12分)甲、乙两名同学在高一学年中(相同条件下)都参加数学考试十次,每次考试成绩如下表:
 次数 次数同学 |
一 |
二 |
三 |
四 |
五 |
六 |
七 |
八 |
九 |
十 |
| 甲 |
90 |
50 |
70 |
80 |
70 |
60 |
80 |
60 |
70 |
70 |
| 乙 |
20 |
40 |
60 |
80 |
70 |
70 |
80 |
90 |
90 |
100 |
请在坐标系中画出甲、乙两同学的成绩折线图,并从以下不同角度对这次测试结果进行分析。
(1)从平均数和方差相结合看,分析谁的成绩更稳定些;
(2)从平均数和中位数相结合看,分析谁的成绩好些;
(3)从平均数和成绩为90分以上的次数相结合看,分析谁的成绩好些 ;
(4)从折线图上两人成绩分数的走势看,分析谁更有潜力。
(满分10分)已知数列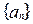 ,
,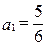 ,若以
,若以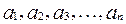 为系数的二次方程
为系数的二次方程 都有根
都有根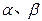 ,且满足
,且满足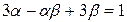 。
。
(1)求数列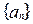 通项公式;
通项公式;
(2)求数列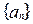 前
前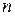 项和
项和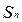 .
.