已知集合 ,
, ,
, ,则
,则 .
.
函数 的最小正周期是 .
的最小正周期是 .
 = .
= .
在等差数列 中,若
中,若 ,则
,则 .
.
若正实数 满足
满足 ,则
,则 的最小值是 ______.
的最小值是 ______.
若方程 的解所在区间为
的解所在区间为 ,则
,则 .
.
设 ,函数
,函数 有意义, 实数
有意义, 实数 取值范围 .
取值范围 .
已知 都是单位向量,且
都是单位向量,且 ,则
,则 的值为 .
的值为 .
已知函数 的图象关于直线
的图象关于直线 对称,则
对称,则 的单调递增区间为 .
的单调递增区间为 .
椭圆中有如下结论:椭圆 上斜率为1的弦的中点在直线
上斜率为1的弦的中点在直线 上,类比上述结论得到正确的结论为:双曲线
上,类比上述结论得到正确的结论为:双曲线 上斜率为1的弦的中点在直线 上.
上斜率为1的弦的中点在直线 上.
设 ,则
,则 的值为 .
的值为 .
函数 在区间
在区间 上的最小值为_________.
上的最小值为_________.
已知 是边长为4的正三角形,
是边长为4的正三角形, 是
是 内部两点,且满足
内部两点,且满足 ,
, ,则
,则 的面积为 .
的面积为 .
已知函数 ,若
,若 ,且
,且 ,则
,则 的最小值是 .
的最小值是 .
如图,正三棱柱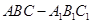 中,点
中,点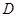 是
是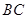 的中点.
的中点.
(Ⅰ)求证: 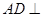 平面
平面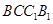 ;
;
(Ⅱ)求证: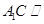 平面
平面 .
.
已知 ,
, .
.
(1)若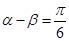 ,求
,求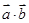 的值;
的值;
(2)若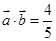 ,
,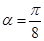 求
求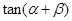 的值.
的值.
如图,在 中,
中, 边上的中线
边上的中线 长为3,且
长为3,且 ,
, .
.
(Ⅰ)求 的值;(Ⅱ)求
的值;(Ⅱ)求 边的长.
边的长.
如图所示,将一矩形花坛 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛 ,要求
,要求 在
在 的延长线上,
的延长线上, 在
在 的延长线上,且对角线
的延长线上,且对角线 过
过 点.已知
点.已知 米,
米, 米。
米。
(1)设 (单位:米),要使花坛
(单位:米),要使花坛 的面积大于32平方米,求
的面积大于32平方米,求 的取值范围;
的取值范围;
(2)若 (单位:米),则当
(单位:米),则当 ,
, 的长度分别是多少时,花坛
的长度分别是多少时,花坛 的面积最大?并求出最大面积.
的面积最大?并求出最大面积.
设二次函数 在区间
在区间 上的最大值、最小值分别是
上的最大值、最小值分别是 ,集合
,集合 .
.
(Ⅰ)若 ,且
,且 ,求
,求 的值;
的值;
(Ⅱ)若 ,且
,且 ,记
,记 ,求
,求 的最小值.
的最小值.
已知数列 中,
中, ,前
,前 和
和
(Ⅰ)求证:数列 是等差数列; (Ⅱ)求数列
是等差数列; (Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)设数列 的前
的前 项和为
项和为 ,是否存在实数
,是否存在实数 ,使得
,使得 对一切正整数
对一切正整数 都成立?若存在,求
都成立?若存在,求 的最小值,若不存在,试说明理由.
的最小值,若不存在,试说明理由.