 = (1,2),按
= (1,2),按 =(3,4)平移后得
=(3,4)平移后得 ,则
,则 的坐标为 ( )
的坐标为 ( )
| A.(4,6) | B.(-2,-2) | C.(1,2) | D.(3,4) |
sin600°的值是 ( )
A. |
B.-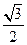 |
C. |
D.-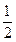 |
已知向量 =(2,3),
=(2,3),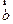 =(-1,2),若m
=(-1,2),若m +
+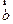 与
与 -2
-2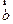 平行,则实数m等于( )
平行,则实数m等于( )
A. |
B. |
C. |
D.- |
已知△ABC中,(1+tanA)(1+tanB)=2,则角C等于 ( )
| A.30° | B.45° | C.135° | D.150° |
已知△ABC中, =
= ,
, =
=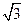 ,A=45°,那么角B等于 ( )
,A=45°,那么角B等于 ( )
| A.30° | B.60° | C.30°或150° | D.60°或120° |
把函数y=cosx的图象上的所有点的横坐标缩小到原来的一半,纵坐标扩大到原来的两倍,然后把图象向左平移 个单位,则所得图象表示的函数为 ( )
个单位,则所得图象表示的函数为 ( )
| A.y=-2sin2x | B.y=2sin2x | C.y=2cos(x+ ) ) |
D.y=2cos( + + ) ) |
函数y=cos2(x+ )-sin2(x+
)-sin2(x+ )是 ( )
)是 ( )
| A.周期为π的奇函数 | B.周期为π的偶函数 |
| C.周期2π的奇函数 | D.周期为2π的偶函数 |
已知向量 =(-2,1),
=(-2,1),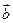 =(-3,0),则
=(-3,0),则 在
在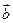 方向上的投影为 ( )
方向上的投影为 ( )
| A.-2 | B.2 | C.- |
D. |
设非零向量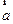 、
、 、
、 满足
满足 ,
, ,则
,则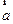 与
与 的夹角是 ( )
的夹角是 ( )
| A.150° | B.120° | C.60° | D.30° |
若点B分 的比为-
的比为- ,且有
,且有 =λ
=λ ,则λ等于( )
,则λ等于( )
| A.2 | B. |
C.1 | D.-1 |
已知点A(3,0),B(0,3),C(cosα,sinα),O(0,0),若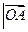 -
-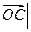 =
= ,α∈(0,π),则
,α∈(0,π),则 ,
, 所成夹角是( )
所成夹角是( )
A. |
B. |
C. |
D. |
已知函数f(x)= (sinx+cosx)-
(sinx+cosx)- |sinx-cosx|,则f(x)的值域是( )
|sinx-cosx|,则f(x)的值域是( )
| A.[-1,1] | B.[- ,1] ,1] |
C.[-1, ] ] |
D.[-1,- ] ] |
已知角α的终边经过点P(m,-3),且cosα=- ,则m= .
,则m= .
在平行四边形ABCD中,AC为一条对角线,若 =(2,4),
=(2,4), =(1,3),则
=(1,3),则 的坐标是 .
的坐标是 .
已知 =3,
=3, =5,如果
=5,如果 ∥
∥ ,则
,则 ·
· =_____________.
=_____________.
对于函数f(x)=cosx+sinx,给出下列四个命题:
(1)存在α∈(0, ),使f(α)=
),使f(α)=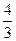 ;
;
(2)存在α∈(0, ),使f(x+α)=f(x+3α)恒成立;
),使f(x+α)=f(x+3α)恒成立;
(3)存在φ∈R,使函数f(x+φ)的图象关于y轴对称;
(4)函数f(x)的图象关于点( ,0)成中心对称;
,0)成中心对称;
其中正确命题的序号是 .
(本小题满分12分)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0, 的部分图像如下图所示:
的部分图像如下图所示:
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)写出函数f(x)的递增区间.
(本小题满分12分)设向量 =(3,1),
=(3,1), =(-1,2),向量
=(-1,2),向量 垂直于向量
垂直于向量 ,向量
,向量 平行于
平行于 ,试求
,试求 时,
时, 的坐标.
的坐标.
(本小题满分12分)如图,设A是单位圆和x轴正半轴的交点,P、Q是单位圆上的两点,O是坐标原点,∠AOP=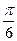 ,∠AOQ=α,α∈[0,π).
,∠AOQ=α,α∈[0,π).
(Ⅰ)若Q( ,
, ),求cos(α-
),求cos(α-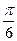 )的值;
)的值;
(Ⅱ)设函数f(α)= ,求f(α)的值域.
,求f(α)的值域.
(本小题满分12分)已知△ABC中,角A,B,C的对边分别为a,b,c,且b= c,sinA•cosC=3sinC•cosA.
c,sinA•cosC=3sinC•cosA.
(Ⅰ)若△ABC的面积S=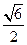 sinA,求c;
sinA,求c;
(Ⅱ)求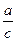 的值.
的值.
(本小题满分12分)在△ABC中,a,b,c分别是角A、B、C的对边, =(2b-c,cosC),
=(2b-c,cosC), =(a,cosA),且
=(a,cosA),且 //
// .
.
(Ⅰ)求角A的大小;
(Ⅱ)求值:sin(A-10°)[1+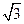 tan(A-50°)];
tan(A-50°)];
(Ⅲ)若a= ,
, +3=0,b<c,求b和c的值.
+3=0,b<c,求b和c的值.
(本小题满分14分)已知平面向量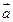 =(
=( ,-1),
,-1), =(x,y)(x>0),
=(x,y)(x>0),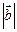 =1.
=1.
(Ⅰ)若对任意实数t都有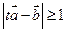 ,求向量
,求向量 ;
;
(Ⅱ)令 =
= +(sin2α-2cos2α)
+(sin2α-2cos2α) ,
, =(
=( sin22α)
sin22α) +(cos2α)
+(cos2α) ,α∈(
,α∈( ,π),若
,π),若 ⊥
⊥ ,
, ,求tanα的值;
,求tanα的值;
(Ⅲ)在(Ⅱ)的条件下,求 的值.
的值.