已知集合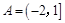 ,
,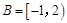 ,则
,则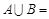 .
.
命题“若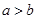 ,则
,则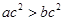 (
( R)”否命题的真假性为 (从“真”、“假”中选填一个).
R)”否命题的真假性为 (从“真”、“假”中选填一个).
已知扇形的周长是8cm,圆心角为2 rad,则扇形的弧长为 cm.
已知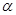 为钝角,且
为钝角,且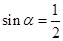 ,则与角
,则与角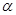 终边相同的角
终边相同的角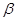 的集合为 .
的集合为 .
集合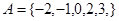 ,集合
,集合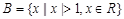 ,集合
,集合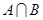 的真子集有 个.
的真子集有 个.
化简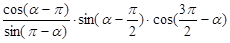 的结果是 .
的结果是 .
已知命题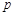 :“正数
:“正数 的平方不等于0”,命题
的平方不等于0”,命题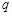 :“若
:“若 不是正数,则它的平方等于0”,
不是正数,则它的平方等于0”,
则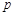 是
是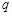 的 .(从“逆命题、否命题、逆否命题、否定”中选一个填空).
的 .(从“逆命题、否命题、逆否命题、否定”中选一个填空).
已知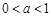 ,则满足
,则满足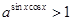 的角
的角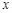 所在的象限为 .
所在的象限为 .
定义在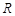 上的函数
上的函数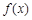 ,对任意
,对任意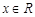 都有
都有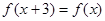 ,当
,当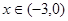 时,
时,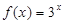 ,则
,则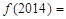 .
.
若函数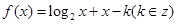 在区间(2,3)上有零点,则
在区间(2,3)上有零点,则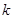 = .
= .
设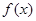 是定义在
是定义在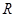 上的奇函数,且
上的奇函数,且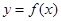 的图像关于直线
的图像关于直线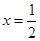 对称,则
对称,则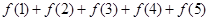 = .
= .
曲线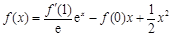 在点
在点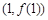 处的切线方程为_________.
处的切线方程为_________.
正实数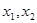 及
及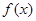 满足
满足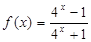 ,且
,且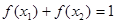 ,则
,则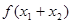 的最小值等于 .
的最小值等于 .
已知平面上的线段 及点
及点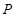 ,任取
,任取 上的一点
上的一点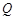 ,线段
,线段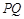 长度的最小值称为点
长度的最小值称为点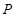 到线段
到线段 的距离,记为
的距离,记为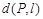 .设
.设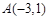 ,
,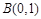 ,
,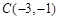 ,
,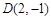 ,
,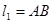 ,
,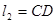 ,若
,若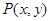 满足
满足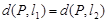 ,则
,则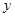 关于
关于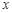 的函数解析式为 .
的函数解析式为 .
(1)设 ,求
,求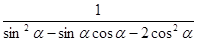 的值;
的值;
(2)已知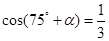 ,且
,且 ,求
,求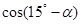 的值.
的值.
已知集合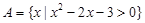 ,
,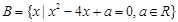 .
.
(1)存在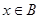 ,使得
,使得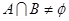 ,求
,求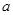 的取值范围;
的取值范围;
(2)若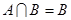 ,求
,求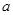 的取值范围.
的取值范围.
已知定义域为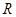 的函数
的函数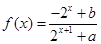 是奇函数.
是奇函数.
(1)求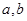 的值;
的值;
(2)判断函数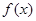 的单调性,并证明.
的单调性,并证明.
(1)设扇形的周长是定值为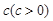 ,中心角
,中心角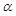 .求证:当
.求证:当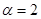 时该扇形面积最大;
时该扇形面积最大;
(2)设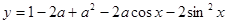
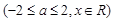 .求证:
.求证: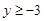 .
.
设 是同时符合以下性质的函数
是同时符合以下性质的函数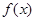 组成的集合:
组成的集合:
①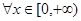 ,都有
,都有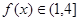 ;②
;②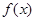 在
在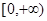 上是减函数.
上是减函数.
(1)判断函数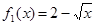 和
和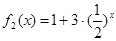 (
(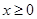 )是否属于集合
)是否属于集合 ,并简要说明理由;
,并简要说明理由;
(2)把(1)中你认为是集合 中的一个函数记为
中的一个函数记为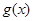 ,若不等式
,若不等式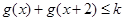 对任意的
对任意的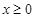 总成立,求实数
总成立,求实数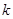 的取值范围.
的取值范围.
已知函数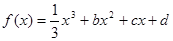 ,设曲线
,设曲线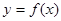 在与
在与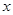 轴交点处的切线为
轴交点处的切线为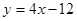 ,
, 为
为 的导函数,满足
的导函数,满足 .
.
(1)求 ;
;
(2)设 ,
,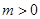 ,求函数
,求函数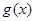 在
在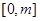 上的最大值;
上的最大值;
(3)设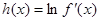 ,若对于一切
,若对于一切 ,不等式
,不等式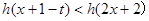 恒成立,求实数
恒成立,求实数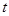 的取值范围.
的取值范围.