设集合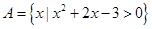 ,
, ,则
,则 =( )
=( )
A.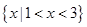 |
B. |
C. |
D.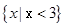 |
已知函数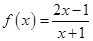 ,则
,则 =( )
=( )
A.在 上单调递增 上单调递增 |
B.在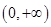 上单调递增 上单调递增 |
C.在  上单调递减 上单调递减 |
D.在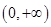 上单调递减 上单调递减 |
如图,运行该程序后输出的 值为( )
值为( ) 
| A.66 | B.55 | C.11 | D.10 |
“ ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知 ,
, ,
, ,则( )
,则( )
| A.a>b>c | B.a>c>b | C.b>c>a | D.c>b>a |
已知 ,则函数
,则函数 的最大值是( )
的最大值是( )
| A.3 | B. |
C. |
D. |
对于空间的两条直线 ,
, 和一个平面
和一个平面 ,下列命题中的真命题是( )
,下列命题中的真命题是( )
A.若 , , ,则 ,则 |
B.若  , , ,则 ,则 |
C.若 , , ,则 ,则 |
D.若 , ,  ,则 ,则 |
等差数列
 中,已知
中,已知 ,且在前
,且在前 项和
项和 中,仅当
中,仅当 时,
时, 最大,则公差d满足( )
最大,则公差d满足( )
A. |
B. |
C. |
D. |
已知平面向量 ,
, ,满足
,满足 ,
, ,
, ,则
,则 =( )
=( )
| A.2 | B.3 | C.4 | D.6 |
已知 ,
, 是椭圆的两个焦点,若椭圆上存在点P,使得
是椭圆的两个焦点,若椭圆上存在点P,使得 ,则椭圆的离心率的取值范围是( )
,则椭圆的离心率的取值范围是( )
A. |
B. |
C. |
D. |
计算:复数 ____________.
____________.
设 的展开式中
的展开式中 项的系数为A,则A=___________.
项的系数为A,则A=___________.
若某空间几何体的三视图如图所示,则该几何体的体积是___________.
已知 ,则
,则 的最大值是________.
的最大值是________.
已知正实数 ,
, 满足
满足 ,则
,则 的最小值是___________.
的最小值是___________.
若直线 与圆
与圆 相切,则实数
相切,则实数 的值是_________.
的值是_________.
已知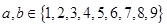 ,
,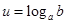 ,则
,则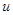 的不同取值个数为_________.
的不同取值个数为_________.
一个袋子中装有6个红球和4个白球,假设每一个球被摸到的可能性是相等的.
(Ⅰ)从袋子中摸出3个球,求摸出的球为2个红球和1个白球的概率;
(Ⅱ)从袋子中摸出两个球,其中白球的个数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
已知等比数列 单调递增,
单调递增, ,
, ,
, .
.
(Ⅰ)求 ;
;
(Ⅱ)若 ,求
,求 的最小值.
的最小值.
如图,三棱锥 中,
中, ,
,

(Ⅰ)求证: ;
;
(Ⅱ)若 ,
, 是
是 的中点,求
的中点,求 与平面
与平面 所成角的正切值
所成角的正切值
如图,已知抛物线 焦点为
焦点为 ,直线
,直线 经过点
经过点 且与抛物线
且与抛物线 相交于
相交于 ,
, 两点
两点 
(Ⅰ)若线段 的中点在直线
的中点在直线 上,求直线
上,求直线 的方程;
的方程;
(Ⅱ)若线段 ,求直线
,求直线 的方程
的方程
已知函数 ,曲线
,曲线 在点
在点 处的切线是
处的切线是 :
:
(Ⅰ)求 ,
, 的值;
的值;
(Ⅱ)若 在
在 上单调递增,求
上单调递增,求 的取值范围
的取值范围