已知集合 ,
, ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
若 ,则
,则 的值为( )
的值为( )
A. |
B. |
C. |
D. |
给出下列命题:
①若“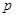 且
且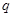 ”为假命题,则
”为假命题,则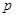 、
、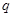 均为假命题;
均为假命题;
② 、
、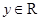 ,
,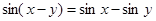 ;
;
③“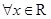 ,
,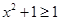 ”的否命题是“
”的否命题是“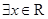 ,
,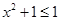 ”;
”;
④在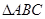 中,“
中,“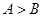 ”是“
”是“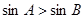 ”的充要条件.
”的充要条件.
其中正确的命题的个数是( )
| A.1 | B.4 | C.3 | D.2 |
函数  的部分图象如图,将
的部分图象如图,将 的图象向右平移
的图象向右平移 个单位长得到函数
个单位长得到函数 的图象,则
的图象,则 的单调增区间为( )
的单调增区间为( )
A. |
B. |
C. |
D. |
已知向量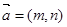 ,
, ,其中
,其中 ,若
,若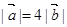 ,当
,当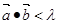 恒成立时实数
恒成立时实数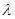 的取值范围是( )
的取值范围是( )
A.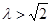 或 或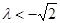 |
B.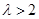 或 或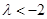 |
C.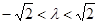 |
D.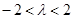 |
若函数 对于任意的
对于任意的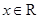 都有
都有 ,且
,且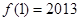 ,则
,则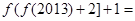 ( )
( )
A. |
B. |
C.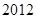 |
D.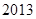 |
在整数集 中,被5整除所得余数为
中,被5整除所得余数为 的所有整数组成一个“类”,记为
的所有整数组成一个“类”,记为 ,
, ,给出如下三个结论:
,给出如下三个结论:
① ;
;
② ;
;
③ ;、
;、
④“整数 、
、 属于同一“类”的充要条件是“
属于同一“类”的充要条件是“ ”.
”.
其中,正确结论的个数是( )
| A. 0 | B. 1 | C.2 | D.3 |
已知定义在 上的函数
上的函数 满足
满足 ,且
,且 的导函数
的导函数 在
在 上恒有
上恒有 ,则不等式
,则不等式 的解集为( )
的解集为( )
A. |
B. |
C. |
D.  |
已知函数 ,
, ,已知当
,已知当 时,函数
时,函数 所有零点和为9,则当
所有零点和为9,则当 时,函数
时,函数 所有零点和为( )
所有零点和为( )
| A.15 | B.12 | C. 9 | D.与 的取值有关 的取值有关 |
设平面向量 ,
, ,若
,若 //
// ,则
,则 .
.
设函数 ,若
,若 是奇函数,则
是奇函数,则 .
.
已知命题 恒成立,命题
恒成立,命题 为减函数,若“
为减函数,若“ ”为真命题,则
”为真命题,则 的取值范围是 .
的取值范围是 .
已知 ,且
,且 ,则
,则 .
.
如图, 为直线
为直线 外一点,若
外一点,若 ,
, ,
, ,
, ,
, ,
, ,
, ,
, 中任意相邻两点的距离相等,设
中任意相邻两点的距离相等,设 ,
, ,用
,用 ,
, 表示
表示 ,其结果为 .
,其结果为 .
运用物理中矢量运算及向量坐标表示与运算,我们知道:两点等分单位圆时,有相应正确关系为 ,三等分单位圆时,有相应正确关系为
,三等分单位圆时,有相应正确关系为 ,由此推出:四等分单位圆时的相应正确关系为 .
,由此推出:四等分单位圆时的相应正确关系为 .
已知函数 ,任取
,任取 ,定义集合
,定义集合 ,点
,点 满足
满足 ,设
,设 ,
, 分别表示集合
分别表示集合 中元素的最大值和最小值,记
中元素的最大值和最小值,记 ,则
,则
(Ⅰ)若函数 ,则
,则 ;
;
(Ⅱ)若函数 ,则
,则 的最小正周期为 .
的最小正周期为 .
已知 ,
, ,
, ,
, 为坐标原点.
为坐标原点.
(Ⅰ) ,求
,求 的值;;
的值;;
(Ⅱ)若 ,且
,且 ,求
,求 与
与 的夹角.
的夹角.
已知 且
且 ,函数
,函数 ,
, ,记
,记 .
.
(Ⅰ)求函数 的定义域
的定义域 的表达式及其零点;
的表达式及其零点;
(Ⅱ)若关于 的方程
的方程 在区间
在区间 内仅有一解,求实数
内仅有一解,求实数 的取值范围.
的取值范围.
设函数 .
.
(Ⅰ)证明: 时,函数
时,函数 在
在 上单调递增;
上单调递增;
(Ⅱ)证明: .
.
已知函数 .
.
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)如果对于任意的 ,
, 总成立,求实数
总成立,求实数 的取值范围;
的取值范围;
(Ⅲ)是否存在正实数 ,使得:当
,使得:当 时,不等式
时,不等式 恒成立?请给出结论并说明理由.
恒成立?请给出结论并说明理由.