已知集合 则 ( )
则 ( )
A.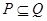 |
B. |
C.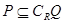 |
D. |
已知:
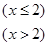 则
则 等于 ( )
等于 ( )
| A.-1 | B.1 | C.-2 | D.2 |
下列函数中,既是偶函数又在 上单调递增的函数是( )
上单调递增的函数是( )
A. |
B.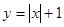 |
C. |
D. |
若奇函数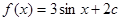 的定义域是
的定义域是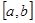 ,则
,则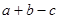 等于( )
等于( )
| A.3 | B.-3 | C.0 | D.无法计算 |
设 ,
, ,
, 则 ( )
则 ( )
A. |
B. |
C. |
D. |
“ ”是“
”是“ ”的 ( )
”的 ( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
如右图是张大爷晨练时所走的离家距离(y)与行走时间(x)之间函数关系的图象,若用黑点表示张大爷家的位置,则张大爷散步行走的路线可能是 ( )

已知函数 在区间
在区间 上是增函数,则实数
上是增函数,则实数 的取值范围是 ( )
的取值范围是 ( )
A. |
B. |
C. |
D. |
函数 的最小正周期为
的最小正周期为 ,且
,且 .当
.当 时
时 ,那么在区间
,那么在区间 上,函数
上,函数 的零点个数( )
的零点个数( )
A. |
B. |
C. |
D. |
设函数 在
在 内有定义,对于给定的正数k,定义函数:
内有定义,对于给定的正数k,定义函数:
 ,取函数
,取函数 ,若对任意的
,若对任意的 ,恒有
,恒有 ,则( )
,则( )
A. 的最大值为2 的最大值为2 |
B. 的最小值为2 的最小值为2 |
C. 的最大值为1 的最大值为1 |
D. 的最小值为1 的最小值为1 |
命题:“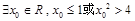 ”的否定是________.
”的否定是________.
若 ,则
,则 ________.
________.
已知命题 :
: [0,l],
[0,l], ,命题
,命题 若命题“
若命题“ ”是真命题,则实数
”是真命题,则实数 的取值范围是 .
的取值范围是 .
关于 的方程
的方程 只有一个实数解,则实数
只有一个实数解,则实数 的取值范围是_______.
的取值范围是_______.
函数 给出四个命题:
给出四个命题:
①当 时,
时, 是奇函数;
是奇函数;
②当 时方程
时方程 只有一个实数根;
只有一个实数根;
③ 的图象关于点
的图象关于点 对称;
对称;
④方程 至多有两个实数根.
至多有两个实数根.
上述命题中,所有正确命题的序号是________.
已知:全集 ,函数
,函数 的定义域为集合
的定义域为集合 ,集合
,集合
(1)求 ;
;
(2)若 ,求实数
,求实数 的范围.
的范围.
已知函数
 是奇函数.
是奇函数.
(1)求实数 的值;
的值;
(2)若函数 在区间
在区间 上单调递增,求实数
上单调递增,求实数 的取值范围;
的取值范围;
(3)求函数 的值域.
的值域.
已知函数 ,
,
(1)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)求函数 的极值.
的极值.
若 的定义域为
的定义域为  ,值域为
,值域为 ,则称函数
,则称函数 是
是 上的“四维方军”函数.
上的“四维方军”函数.
(1)设 是
是 上的“四维方军”函数,求常数
上的“四维方军”函数,求常数 的值;
的值;
(2)问是否存在常数 使函数
使函数 是区间
是区间 上的“四维方军”函数?若存在,求出
上的“四维方军”函数?若存在,求出 的值,否则,请说明理由.
的值,否则,请说明理由.
设函数

(1)求 的单调区间、最大值;
的单调区间、最大值;
(2)讨论关于 的方程
的方程 的根的个数.
的根的个数.
已知 ,若矩阵
,若矩阵 所对应的变换把直线
所对应的变换把直线 :
: 变换为自身,求
变换为自身,求 .
.
求圆 被直线
被直线 (
( 是参数)截得的弦长.
是参数)截得的弦长.
已知函数 ,
,
①若不等式 的解集为
的解集为 ,求实数
,求实数 的值;
的值;
②在①的条件下,若 对一切实数
对一切实数 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.