已知集合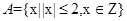 ,
, ,则
,则 是( )
是( )
A. |
B. |
C. |
D. |
已知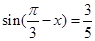 ,则
,则 ( )
( )
A. |
B. |
C.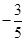 |
D. |
下列给出的四个命题中,说法正确的是( )
A.命题“若 ,则 ,则 ”的否命题是“若 ”的否命题是“若 ,则 ,则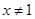 ”; ”; |
B.“ ”是“ ”是“ ”的必要不充分条件; ”的必要不充分条件; |
C.命题“存在 ,使得 ,使得 ”的否定是“对任意 ”的否定是“对任意 ,均有 ,均有 ”; ”; |
D.命题“若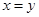 ,则 ,则 ”的逆否命题为真. ”的逆否命题为真. |
把函数 的图像上所有的点向左平移
的图像上所有的点向左平移 个单位长度,再把图像上所有点的横坐标伸长到原来的2倍(纵坐标不变)得到的图像所表示的函数为( )
个单位长度,再把图像上所有点的横坐标伸长到原来的2倍(纵坐标不变)得到的图像所表示的函数为( )
A. |
B.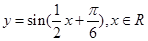 |
C. |
D. |
已知 的图像如图所示,则函数
的图像如图所示,则函数 的图像是( )
的图像是( )

已知 ,
, ,
, ,
, ,则
,则 的大小关系为( )
的大小关系为( )
A. |
B.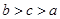 |
C. |
D. |
某出租车公司计划用450万元购买A型和B型两款汽车投入营运,购买总量不超过50辆,其中购买A型汽车需要13万元/辆,购买B型汽车需要8万元/辆,假设公司第一年A型汽车的纯利润为5万元/辆,B型汽车的纯利润为1.5万元/辆,为使该公司第一年纯利润最大,则需安排购买( )
| A.8辆A型汽车,42辆B型汽车 | B.9辆A型汽车,41辆B型汽车 |
| C.11辆A型汽车,39辆B型汽车 | D.10辆A型汽车,40辆B型汽车 |
已知二次函数 的导数为
的导数为 ,
, ,
, 与
与 轴恰有一个交点,则
轴恰有一个交点,则 的最小值为( )
的最小值为( )
| A.3 | B. |
C.2 | D. |
设 ,若
,若 ,则
,则 的最大值为( )
的最大值为( )
| A.2 | B.3 | C.4 | D. |
在直角坐标系中,定义两点 之间的“直角距离”为
之间的“直角距离”为 ,
,
现给出四个命题:
①已知 ,则
,则 为定值;
为定值;
②用 表示
表示 两点间的“直线距离”,那么
两点间的“直线距离”,那么 ;
;
③已知 为直线
为直线 上任一点,
上任一点, 为坐标原点,则
为坐标原点,则 的最小值为
的最小值为 ;
;
④已知 三点不共线,则必有
三点不共线,则必有 .
.
| A.②③ | B.①④ | C.①② | D.①②④ |
 .
.
不等式组 的解集为 .
的解集为 .
在极坐标系中,设 是直线
是直线 上任一点,
上任一点, 是圆
是圆 上任一点,则
上任一点,则 的最小值为 .
的最小值为 .
若函数 的一个正数零点附近的函数值用二分法计算,其参考数据如下:
的一个正数零点附近的函数值用二分法计算,其参考数据如下:
那么方程 的一个近似根(精确到0.1)为
的一个近似根(精确到0.1)为
定义在 上的函数
上的函数 ,满足
,满足 ,
,
(1)若 ,则
,则 .
.
(2)若 ,则
,则 (用含
(用含 的式子表示).
的式子表示).
函数 的最小正周期为
的最小正周期为 ,其图像经过点
,其图像经过点
(1)求 的解析式;
的解析式;
(2)若 且
且 为锐角,求
为锐角,求 的值.
的值.
已知函数
(1)计算 的值,据此提出一个猜想,并予以证明;
的值,据此提出一个猜想,并予以证明;
(2)证明:除点(2,2)外,函数 的图像均在直线
的图像均在直线 的下方.
的下方.
已知角 是
是 的内角,
的内角, 分别是其对边长,且
分别是其对边长,且 .
.
(1)若 ,求
,求 的长;
的长;
(2)设 的对边
的对边 ,求
,求 面积的最大值.
面积的最大值.
已知二次函数 满足
满足 且
且 的图像在
的图像在 处的切线垂直于直线
处的切线垂直于直线 .
.
(1)求 的值;
的值;
(2)若方程 有实数解,求
有实数解,求 的取值范围.
的取值范围.
某校内有一块以 为圆心,
为圆心, (
( 为常数,单位为米)为半径的半圆形(如图)荒地,该校总务处计划对其开发利用,其中弓形
为常数,单位为米)为半径的半圆形(如图)荒地,该校总务处计划对其开发利用,其中弓形 区域(阴影部分)用于种植学校观赏植物,
区域(阴影部分)用于种植学校观赏植物, 区域用于种植花卉出售,其余区域用于种植草皮出售.已知种植学校观赏植物的成本是每平方米20元,种植花卉的利润是每平方米80元,种植草皮的利润是每平方米30元.
区域用于种植花卉出售,其余区域用于种植草皮出售.已知种植学校观赏植物的成本是每平方米20元,种植花卉的利润是每平方米80元,种植草皮的利润是每平方米30元.
(1)设 (单位:弧度),用
(单位:弧度),用 表示弓形
表示弓形 的面积
的面积 ;
;
(2)如果该校总务处邀请你规划这块土地,如何设计 的大小才能使总利润最大?并求出该最大值.
的大小才能使总利润最大?并求出该最大值.
(参考公式:扇形面积公式 ,
, 表示扇形的弧长)
表示扇形的弧长)
已知函数 ,
, ,
, .
.
(1)求 的最大值;
的最大值;
(2)若对 ,总存在
,总存在 使得
使得 成立,求
成立,求 的取值范围;
的取值范围;
(3)证明不等式: .
.